
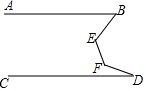
 如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.
如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | (2,0) | B. | (4,0) | C. | (-2,0) | D. | (0,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 两个圆柱形薄玻璃杯(杯身、杯底厚度不计),大杯直径是小杯直径的2倍,把小杯放入大杯中组合成一个容器,其主视图如图所示,现往小杯口中匀速注水,注水过程中杯子始终竖直放置,则下列能反映该容器最高水位h与注水时间t之间关系的大致图象是( )
两个圆柱形薄玻璃杯(杯身、杯底厚度不计),大杯直径是小杯直径的2倍,把小杯放入大杯中组合成一个容器,其主视图如图所示,现往小杯口中匀速注水,注水过程中杯子始终竖直放置,则下列能反映该容器最高水位h与注水时间t之间关系的大致图象是( )| A. | 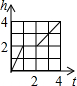 | B. |  | C. | 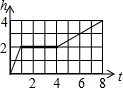 | D. | 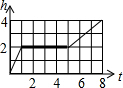 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
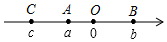 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届浙江省九年级3月模拟数学试卷(解析版) 题型:填空题
函数yl=x ( x≥0 ) ,  (x>0)的图象如图所示,则以下四个结论:① 两函数图象的交点A的坐标为(3 , 3 ) ;② 当 x>3时 ,y2>yl;③ 当 x =1时, BC = 8;④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是________.
(x>0)的图象如图所示,则以下四个结论:① 两函数图象的交点A的坐标为(3 , 3 ) ;② 当 x>3时 ,y2>yl;③ 当 x =1时, BC = 8;④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com