
 足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.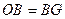 ,求证:四边形OCBD是菱形.
,求证:四边形OCBD是菱形.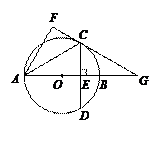

 . ………………………………………1分
. ………………………………………1分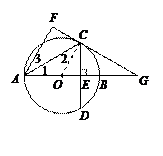

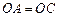 , ∴
, ∴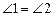 …………………………………………1分
…………………………………………1分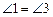 ,
, .…1分
.…1分 . …………………………………1分
. …………………………………1分 .…………………………1分
.…………………………1分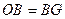 ,∴
,∴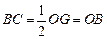 , …………1分
, …………1分 ∴
∴
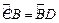 ………………………1分
………………………1分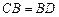 ………………………1分
………………………1分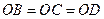
 . ………………………1分
. ………………………1分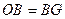 ,∴
,∴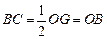 ,………………1分
,………………1分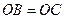 ,∴
,∴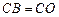 ………………………1分
………………………1分 CD, ∴
CD, ∴ ………………………1分
………………………1分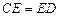 ………………………1分
………………………1分

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:不详 题型:解答题
 图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连
图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连 接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.
接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过. 为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子,?
为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子,?
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 O是△ABC的外接圆,AB = AC,过点A作AP∥BC,交BO的延长线于P.
O是△ABC的外接圆,AB = AC,过点A作AP∥BC,交BO的延长线于P. O的切线;
O的切线; O的半径R = 6,△ACD为等边三角形时,求线段AP的长.
O的半径R = 6,△ACD为等边三角形时,求线段AP的长. 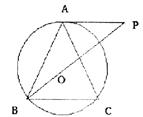
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com