
分析 根据$\sqrt{{x^2}-5x+4}-\sqrt{1-x}=0$,先移项然后两边平方转化为有理方程,进行解答,还要注意根号里面的式子要大于等于零,从而可以进一步确定x的取值范围,本题得以解决.
解答 解:$\sqrt{{x^2}-5x+4}-\sqrt{1-x}=0$,
$\sqrt{{x}^{2}-5x+4}=\sqrt{1-x}$,
两边平方,得
x2-5x+4=1-x,
解得x1=1,x2=3,
又∵$\left\{\begin{array}{l}{{x}^{2}-5x+4≥0}\\{1-x≥0}\end{array}\right.$,
解得x≤1,
∴x=1,
检验:当x=1时,$\sqrt{{1}^{2}-5×1+4}-\sqrt{1-1}=0+0=0$,
故方程$\sqrt{{x^2}-5x+4}-\sqrt{1-x}=0$的解是x=1.
点评 本题考查解无理方程,解题的关键是利用转化的数学思想将无理方程转化为有理方程,注意根号里的式子要大于等于零.


科目:初中数学 来源: 题型:选择题
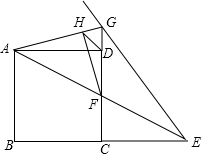 如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=2时,作FH⊥AG于H,连接DH,则DH的长为( )
如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=2时,作FH⊥AG于H,连接DH,则DH的长为( )| A. | 2-$\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -52=(-5)×(-5) | B. | 32=3×2 | C. | 32=3+3 | D. | -(-$\frac{1}{2}$)2=-$\frac{1}{2}$×$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
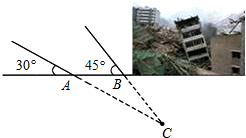 一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)
一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
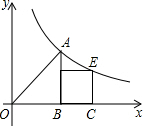 在平面直角坐标系中,等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上,函数y=$\frac{k}{x}$(k>0)的图象过点A,E.若BC=1,则k的值等于$\frac{3+\sqrt{5}}{2}$.
在平面直角坐标系中,等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上,函数y=$\frac{k}{x}$(k>0)的图象过点A,E.若BC=1,则k的值等于$\frac{3+\sqrt{5}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com