
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车.经市场调查得知,购买6辆男式单车与8辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16 000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单车比女式单车多5辆,两种单车至少需要22辆,购置两种单车的费用不超过50 000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
【答案】(1)男式单车2000元/辆,女式单车1500元/辆;(2)该社区共有三种购置方案,其中购置男式单车13辆、女式单车9辆时所需总费用最低,最低费用为41500元.
【解析】
(1)设男式单车x元/辆,女式单车y元/辆,根据“购买6辆男式单车与8辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元”列方程组求解可得;
(2)设购置女式单车m辆,则购置男式单车(m+5)辆,根据“两种单车至少需要22辆、购置两种单车的费用不超过50000元”列不等式组求解,得出m的范围,即可确定购置方案;再列出购置总费用关于m的函数解析式,利用一次函数性质结合m的范围可得其最值情况.
解:(1)设男式单车x元/辆,女式单车y元/辆,
根据题意,得![]() ,
,
解得:![]() ,
,
答:男式单车2000元/辆,女式单车1500元/辆;
(2)设购置女式单车m辆,则购置男式单车(m+5)辆,根据题意,得:
![]() ,
,
解得:8![]() ≤m≤11
≤m≤11![]() ,
,
∵m为整数,
∴m的值可以是9、10、11,即该社区有三种购置方案;
设购置总费用为W,
则W=2000(m+5)+1500m=3500m+10000,
∵3500>0,W随m的增大而增大,
∴当m=9时,W取得最小值,最小值为41500,
答:该社区共有三种购置方案,其中购置男式单车13辆、女式单车9辆时所需总费用最低,最低费用为41500元.


科目:初中数学 来源: 题型:
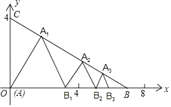
【题目】如图,已知,点A(0,0)、B(4![]() ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
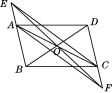
【题目】如图,在ABCD中,点O是AC与BD的交点,过点O的直线与BA的延长线,DC的延长线分别交于点E,F.
(1)求证:△AOE≌△COF.
(2)连接EC,AF,则EF与AC满足什么数量关系时,四边形AECF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
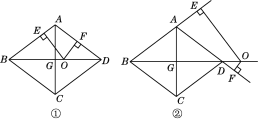
【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
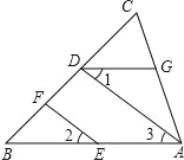
【题目】列推理过程:如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD 的度数.
∵ EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)
∴∠1=∠3(等量代换)
∴ AB∥ ( )
∴∠BAC+ =180°(两直线平行 ,同旁内角互补)
∵∠BAC=80°(已知)
∴∠AGD=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一”儿童节促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com