
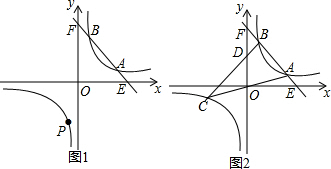
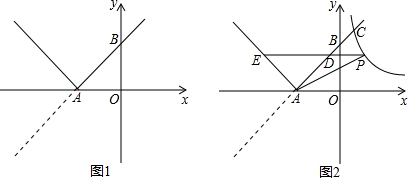
���� ��1��ֻ��ѵ�A��������뷴���������Ľ���ʽ���Ϳ���������������Ľ���ʽ����һ�κ����뷴���������Ľ���ʽ��ɵķ����飬�Ϳɵõ���B�����ꣻ
��2����PAB����ABΪֱ�DZߵ�ֱ�������Σ��ɷ�����������ۣ�������BAP=90�㣬����A��AH��OE��H����AP��x��Ľ���ΪM����ͼ1����OE=5��OH=4��AH=2��HE=1����֤��AHM�ס�EHA���������������ε����ʿ����MH���Ӷ��õ���M�����꣬Ȼ���ô���ϵ�������ֱ��AP�Ľ���ʽ���ٽ�ֱ��AP�뷴���������Ľ���ʽ��ɵķ����飬�Ϳɵõ���P�����ꣻ������ABP=90�㣬ͬ�����ɵõ���P�����ꣻ
��3������B��BS��y����S������C��CT��y����T������OB����ͼ2����֤��CTD�ס�BSD���������������ε����ʿɵ�$\frac{CT}{BS}$=$\frac{CD}{BD}$=$\frac{3}{2}$����A��a��-2a+10����B��b��-2b+10�����ɵ�C��-a��2a-10����CT=a��BS=b�����ɵõ�$\frac{a}{b}$=$\frac{3}{2}$����b=$\frac{2}{3}$a����A��B���ڷ�����������ͼ���Ͽɵ�a��-2a+10��=b��-2b+10������b=$\frac{2}{3}$a���뼴�����a��ֵ���Ӷ��õ���A��B��C�����꣬���ô���ϵ�������ֱ��BC�Ľ���ʽ���Ӷ��õ���D�����꼰OD��ֵ��Ȼ�����ø�������S��COB������OA=OC�ɵ�S��ABC=2S��COB��������Խ����
��� �⣺��1����A��4��2������y=$\frac{k}{x}$����k=4��2=8��
�෴���������Ľ���ʽΪy=$\frac{8}{x}$��
�ⷽ����$\left\{\begin{array}{l}{y=-2x+10}\\{y=\frac{8}{x}}\end{array}\right.$����
$\left\{\begin{array}{l}{x=1}\\{y=8}\end{array}\right.$��$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$��
���B��������1��8����
��2��������BAP=90�㣬
����A��AH��OE��H����AP��x��Ľ���ΪM����ͼ1��
����y=-2x+10��
��y=0ʱ��-2x+10=0�����x=5��
���E��5��0����OE=5��
��A��4��2������OH=4��AH=2��
��HE=5-4=1��
��AH��OE�����AHM=��AHE=90�㣮
�֡ߡ�BAP=90�㣬
���AME+��AEM=90�㣬��AME+��MAH=90�㣬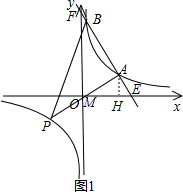
���MAH=��AEM��
���AHM�ס�EHA��
��$\frac{AH}{EH}$=$\frac{MH}{AH}$��
��$\frac{2}{1}$=$\frac{MH}{2}$��
��MH=4��
��M��0��0����
����ֱ��AP�Ľ���ʽΪy=mx
����4m=2�����m=$\frac{1}{2}$��
��ֱ��AP�Ľ���ʽΪy=$\frac{1}{2}$x��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=\frac{8}{x}}\end{array}\right.$����
$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$��$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$��
���P��������-4��-2����
������ABP=90�㣬
ͬ���ɵã���P������Ϊ��-16��-$\frac{1}{2}$����
�������������������ĵ�P������Ϊ��-4��-2������-16��-$\frac{1}{2}$����
��3������B��BS��y����S������C��CT��y����T������OB����ͼ2��
����BS��CT��
���CTD�ס�BSD��
��$\frac{CD}{BD}$=$\frac{CT}{BS}$��
��$\frac{BC}{BD}$=$\frac{5}{2}$��
��$\frac{CT}{BS}$=$\frac{CD}{BD}$=$\frac{3}{2}$��
��A��a��-2a+10����B��b��-2b+10����
��C��-a��2a-10����CT=a��BS=b��
��$\frac{a}{b}$=$\frac{3}{2}$����b=$\frac{2}{3}$a��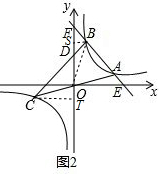
��A��a��-2a+10����B��b��-2b+10�����ڷ���������y=$\frac{k}{x}$��ͼ���ϣ�
��a��-2a+10��=b��-2b+10����
��a��-2a+10��=$\frac{2}{3}$a��-2��$\frac{2}{3}$a+10����
��a��0��
��-2a+10=$\frac{2}{3}$��-2��$\frac{2}{3}$a+10����
��ã�a=3��
��A��3��4����B��2��6����C��-3��-4����
��ֱ��BC�Ľ���ʽΪy=px+q��
����$\left\{\begin{array}{l}{2p+q=6}\\{-3p+q=-4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{p=2}\\{q=2}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=2x+2��
��x=0ʱ��y=2�����D��0��2����OD=2��
��S��COB=S��ODC+S��ODB
=$\frac{1}{2}$OD•CT+$\frac{1}{2}$OD•BS
=$\frac{1}{2}$��2��3+$\frac{1}{2}$��2��2=5��
��OA=OC��
��S��AOB=S��COB��
��S��ABC=2S��COB=10��
���� ������Ҫ���������ô���ϵ��������������һ�κ����Ľ���ʽ������������һ�κ���ͼ��Ľ��㡢�����ε�����ƽ�������ε���������������ε��ж������ʡ���������ǵ����ʡ�ֱ������������ǻ����֪ʶ���ڽ������Ĺ����У��õ��˷������ۡ����ν�ϡ��������Ҫ����ѧ˼�뷽����Ӧ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
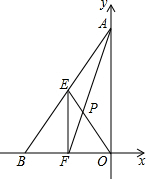 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��B������ֱ�Ϊ��0��4������-3��0������E��F�ֱ�ΪAB��BO���е㣬�ֱ�����AF��EO������ΪP����P������Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��B������ֱ�Ϊ��0��4������-3��0������E��F�ֱ�ΪAB��BO���е㣬�ֱ�����AF��EO������ΪP����P������Ϊ��������| A�� | ��-1��$\frac{4}{3}$�� | B�� | ��-$\frac{3}{2}$��2�� | C�� | ��-$\frac{3}{2}$��$\frac{4}{3}$�� | D�� | ��-1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
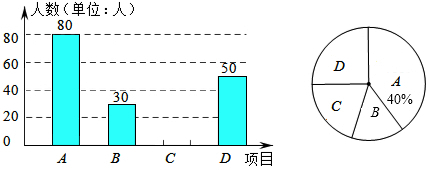
| A�� | 240 | B�� | 120 | C�� | 80 | D�� | 40 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1��x��2 | B�� | 1��x��2 | C�� | -1��x��2 | D�� | -1��x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com