
【题目】如图,抛物线![]() 过点
过点![]() ,且与直线
,且与直线![]() 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为![]() .
.

(1)求抛物线的解析式;
(2)点D为抛物线上位于直线![]() 上方的一点,过点D作
上方的一点,过点D作![]() 轴交直线
轴交直线![]() 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的最小值;
的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]() ;(3)点Q的坐标:
;(3)点Q的坐标:![]() 、
、![]() .
.
【解析】
(1)将点B的坐标为![]() 代入
代入![]() ,
,![]() ,B的坐标为
,B的坐标为![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,解得
,解得![]() ,
,![]() ,因此抛物线的解析式
,因此抛物线的解析式![]() ;
;
(2)设![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() 有最大值为2,此时
有最大值为2,此时![]() ,作点A关于对称轴的对称点
,作点A关于对称轴的对称点![]() ,连接
,连接![]() ,与对称轴交于点P.
,与对称轴交于点P.![]() ,此时
,此时![]() 最小;
最小;
(3)作![]() 轴于点H,连接
轴于点H,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,
,![]() 因为
因为![]() ,
,![]() ,所以
,所以![]() ,可知
,可知![]() 外接圆的圆心为H,于是
外接圆的圆心为H,于是![]() 设
设![]() ,则
,则![]() ,
,![]() 或
或![]() ,求得符合题意的点Q的坐标:
,求得符合题意的点Q的坐标:![]() 、
、![]() .
.
解:(1)将点B的坐标为![]() 代入
代入![]() ,
,
![]() ,
,
∴B的坐标为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
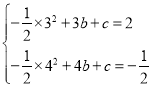
解得![]() ,
,![]() ,
,
∴抛物线的解析式![]() ;
;
(2)设![]() ,则
,则![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 有最大值为2,
有最大值为2,
此时![]() ,
,
作点A关于对称轴的对称点![]() ,连接
,连接![]() ,与对称轴交于点P.
,与对称轴交于点P.
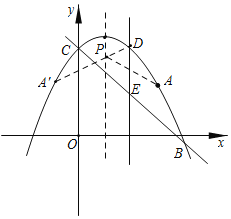
![]() ,此时
,此时![]() 最小,
最小,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
即![]() 的最小值为
的最小值为![]() ;
;
(3)作![]() 轴于点H,连接
轴于点H,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
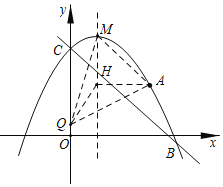
∵抛物线的解析式![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
![]() ,
,
∴![]() ,
,
可知![]() 外接圆的圆心为H,
外接圆的圆心为H,
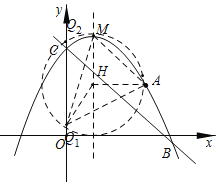
∴![]()
设![]() ,
,
则![]() ,
,
![]() 或
或![]()
∴符合题意的点Q的坐标:![]() 、
、![]() .
.


科目:初中数学 来源: 题型:
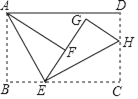
【题目】如图,矩形ABCD中,AB=4,AD=6,点E为BC上一点,将△ABE沿AE折叠得到△AEF,点H为CD上一点,将△CEH沿EH折叠得到△EHG,且F落在线段EG上,当GF=GH时,则BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=![]() (x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
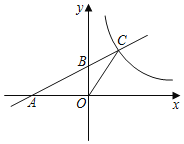
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x
x![]() +
+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.

(1)判断△ABC的形状,并说明理由;
(2)经过B. C两点的直线交抛物线的对称轴于点D,求D点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
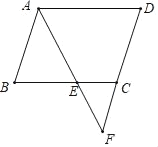
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.
(1)若AB=4,BC=6,求EC的长;
(2)若∠EAD=50°,求∠BAE和∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
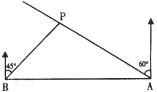
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com