
【题目】具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A= ![]() ∠B=
∠B= ![]() ∠C
∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
【答案】D
【解析】解答:A项,∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴2∠C=180°,解得∠C=90°,∴△ABC是直角三角形,∴本选项错误;
B项,设∠A=x,∠B=2x,∠C=3x,∵∠A+∠B+∠C=180°,∴x+2x+3x=180°,解得x=30°,∴∠C=90°,∴本选项错误;
C项,设∠A=x,∠B=2x,∠C=3x,∵∠A+∠B+∠C=180°,∴x+2x+3x=180°,解得x=30°,∴∠C=90°,∴本选项错误;
D项,∵∠A+∠B+∠C=180°,而∠A=2∠B=3∠C,∴3∠C+ ![]() ∠C+∠C=180°,解得∠C=
∠C+∠C=180°,解得∠C= ![]() ,∴∠A=3∠C=
,∴∠A=3∠C= ![]() ,∴本题选项正确.
,∴本题选项正确.
分析:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键;根据三个角的数量关系即可判断三角形的形状:若两个角的和等于第三个角,则该三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,E,F分别在AB,AC上,则下列各式不能成立的是( ) 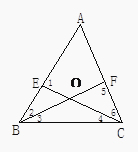
A.∠BOC=∠2+∠6+∠A
B.∠2=∠5-∠A
C.∠5=∠1+∠4
D.∠1=∠ABC+∠4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;
⑤∠BDC= ![]() ∠BAC.
∠BAC.
其中正确的结论有( )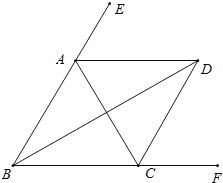
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式与2x-(-3y-4z)相等的是( )
A. 2x+(-3y+4z) B. 2x+(3y+4z)
C. 2x+(3y-4z) D. 2x+(-3y-4z)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠ADC=α,P为直线CD上一动点,点M在线段BC上,连MP,∠MPD=β 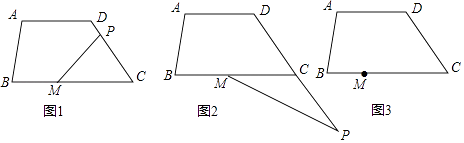
(1)如图,若MP⊥CD,α=120°,则∠BMP=;
(2)如图,当P点在DC延长线上时,∠BMP=;
(3)如图,当P点在CD延长线上时,请画出图形,写出∠BMP、β、α之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
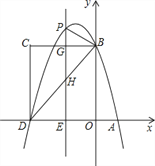
【题目】如图,在平面直角坐标系中,抛物线y=-![]() x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(-3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(-3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 近似数25.0的精确度与近似数25的精确度一样
B. 近似数5千克的精确度和近似数5000克的精确度一样
C. 近似数1.4×104的精确度与近似数14千的精确度一样
D. 今天的温度是28 ℃,那么28 ℃是准确数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com