
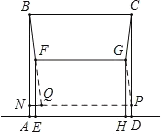
【题目】如图,正方形ABCD与矩形EFGH在直线![]() 的同侧,边AD,EH在直线
的同侧,边AD,EH在直线![]() 上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线
上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线![]() 左右移动,连接BF、CG,则BF+CG的最小值为( )
左右移动,连接BF、CG,则BF+CG的最小值为( )

A. 4B. ![]() C.
C. ![]() D. 5
D. 5
【答案】B
【解析】
作点C关于FG的对称点P,连接GP,以FG,PG为邻边作平行四边形PGFQ,则BF+CG=BF+QF,当B,F,Q三点共线时,BF+CG的最小值为BQ的长,过点Q作QN⊥AB于N,依据勾股定理即可得到在Rt△BNQ中,BQ=![]() ,即可得出BF+CG的最小值为
,即可得出BF+CG的最小值为![]() .
.
解:如图所示,作点C关于FG的对称点P,连接GP,
以FG,PG为邻边作平行四边形PGFQ,则FQ=PG=CG,FG=QP=4,
∴BF+CG=BF+QF,
∴当B,F,Q三点共线时,BF+CG的最小值为BQ的长,
过点Q作QN⊥AB于N,
由题可得BN=2(53)=4,NQ=54=1,
∴Rt△BNQ中,BQ=![]() ,
,
∴BF+CG的最小值为![]() ,
,
故选B.


科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是∠
是∠![]() 内的一点,过点
内的一点,过点![]() 作
作![]() 于点
于点![]() 于点
于点![]() ,且
,且![]() .
.
![]() 求证:
求证: ![]() ;
;
![]() 如图②,点
如图②,点![]() 是射线
是射线![]() 上一点,点
上一点,点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,若
,若![]() .求线段
.求线段![]() 的长.
的长.
![]() 如图③,若
如图③,若![]() ,将
,将![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,
的速度顺时针旋转,![]() 秒后,
秒后,![]() 开始绕点
开始绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,
的速度顺时针旋转,![]() 旋转
旋转![]() 后停止,此时
后停止,此时![]() 也随之停止旋转。旋转过程中,
也随之停止旋转。旋转过程中,![]() 所在直线与
所在直线与![]() 所在直线的交点记为
所在直线的交点记为![]() 所在直线与
所在直线与![]() 所在直线的交点记为
所在直线的交点记为![]() .问
.问![]() 旋转几秒时,
旋转几秒时,![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
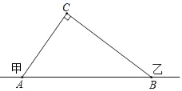
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠CAB=2∠B,AE平分∠CAB,CD⊥AB于D,AC=3,AD=1.下列结论:①∠AEC=∠CAB;②EF=CE;③AC=AE;④BD=4;

正确的是___________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成不完整的统计表,请根据图表中的信息解答下列问题.
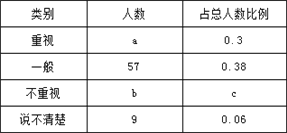
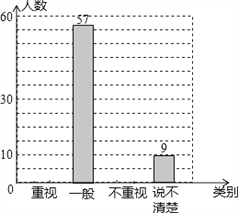
(1)样本容量为 ,表格中c的值为 ,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数为 ;
(3)根据上面的数据统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据![]() ,
, ![]() ,
, ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
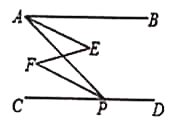
【题目】完成下面的证明.
如图、![]() 与
与![]() 互补,
互补,![]() ,求证:
,求证:![]() .对于本题小丽是这样证明的,请你将她的证明过程补充完整.
.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
证明:![]() 与
与![]() 互补,(已知)
互补,(已知)
![]() .(________________________________)
.(________________________________)
![]() .(________________________________)
.(________________________________)
![]() ,(已知)
,(已知)
![]() ,(等量代换)
,(等量代换)
即_______________=_______________.
![]() .(________________________________)
.(________________________________)
![]() .(________________________________)
.(________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,后解答:
(1)由根式的性质计算下列式子得:
①![]() =3,②
=3,②![]() ,③
,③![]() ,④
,④![]() =5,⑤
=5,⑤![]() =0.
=0.
由上述计算,请写出![]() 的结果(a为任意实数).
的结果(a为任意实数).
(2)利用(1)中的结论,计算下列问题的结果:
①![]() ;
;
②化简:![]() (x<2).
(x<2).
(3)应用:
若![]() =3,求x的取值范围.
=3,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com