
【题目】以下是两张不同类型火车的车票(“Dxxxx次”表示动车,“GXXXX次”表示高铁):
(1)根据车票中的信息填空:该列动车和高铁是向而行(填“相”或“同”).
(2)已知该动车和高铁的平均速度分别为200km/h、300km/h,两列火车的车身长度不计.
①经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到1小时,求A、B两地之间的距离(温馨提醒:注意两张火车票的发车时间).
②在①中测算的数据基础上,已知A、B两地途中依次设有5个站点P1、P2、P3、P4、P5 , 且AP1=P1P2=P2P3=P3P4=P4P5=P5B,动车每个站点都停靠,高铁只停靠P2、P4两个站点,两列火车在每个停靠站点都停留5分钟.求该列高铁追上动车的时刻.
【答案】
(1)同
(2)解:①设A、B两地之间的距离为x km,
根据题意得:![]() ,
,
解得:x=1200.
答:A、B两地之间的距离为1200 km.
②每个相邻站点距离为1200![]() 6=200 km,
6=200 km,
动车到达每一站所花的时间为200![]() 200
200![]() 60=60分钟,
60=60分钟,
高铁到达每一站所花的时间为200![]() 300
300![]() 60=40分钟,
60=40分钟,
∵60![]() (60-40)=3,
(60-40)=3,
∴高铁在P2、P3之间追上动车.
设高铁经过y小时后追上动车,
根据题意得:(y-![]() )
)![]() 300=(y+1-
300=(y+1-![]()
![]() 2)
2)![]() 200,
200,
解得:y=![]() ,
,
∵![]() 小时=1小时55分钟,
小时=1小时55分钟,
∴高铁在8:55追上动车.
答:高铁追上动车的时刻为8:55.
【解析】(1)∵动车和高铁均从A地到B地,
∴两车方向相同.
故答案为:同.(1)根据两车的出发地及目的地,得出结论即可;(2)①设A、B两地之间的距离为x km,根据高铁比动车晚出发1小时,又早到1小时,列车方程,解方程得出结论;②根据AP1=P1P2=P2P3=P3P4=P4P5=P5B,可求出每个相邻站点的距离,结合两车出发的时间及停靠站点休息时间可得出高铁在P2、P3之间追上动车. 再根据等量关系,列出方程,求解,换算成时刻即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点( 2,-3 )关于y轴对称的点的坐标是( )
A. ( -2,3 )B. ( -2,-3 )C. ( 2,3 )D. ( 2,-3 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,正确的是( )
A.单项式 ![]() 的系数是3,次数是2
的系数是3,次数是2
B.单项式m的次数是1,没有系数
C.单项式-xy2z的系数是一1,次数是4
D.多项式2x2+xy+3是四次三项式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,同学们的学习习惯也有了改变,一些同学在做题遇到困难时,喜欢上网查找答案.针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图.
请根据图中提供的信息,解答下列问题:

(1)此次抽样调查中,共调查了多少名学生?
(2)将图1补充完整;
(3)求出扇形统计图中持“反对”意见的学生所在扇形的圆心角的度数;
(4)根据抽样调查结果,请你估计该校1500名学生中有多少名学生持“无所谓”意见.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明借到一本有72页的图书,要在10天之内读完,开始2天每天只读5页,那么以后几天里每天至少要读多少页?设以后几天里每天要读x页,所列不等式为( )
A. 10+8x≥72 B. 2+10x≥72
C. 10+8x≤72 D. 2+10x≤72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,E是CD的中点,F是BC上的一点,且∠AEF=90°,延长AE交BC的延长线于点G.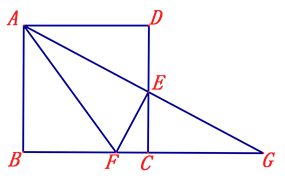
(1)求GE的长;
(2)求证:AE平分∠DAF;
(3)求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
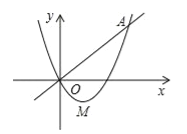
【题目】如图,在平面直角坐标系xOy中,一次函数y=x与二次函数![]() 的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为![]() 的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
(3)直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江涛同学统计了他家10月份的长途电话明细清单,按通话时间画出频数分布直方图.
(1)他家这个月一共打了 次长途电话;
(2)通话时间不足10分钟的 次;
(3)通话时间在分钟范围最多,通话时间在分钟范围最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com