Question

【题目】如图，在边长为4的正方形ABCD中，E是CD的中点，F是BC上的一点，且∠AEF=90°，延长AE交BC的延长线于点G.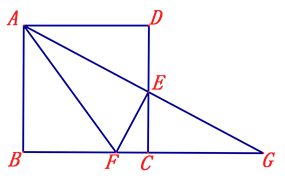

（1）求GE的长；
（2）求证：AE平分∠DAF；
（3）求CF的长.

Answer 1

【答案】
（1）

解：在正方形ABCD中，∠D=90°，AD∥BC

∴∠D=∠DCG=90°，∠DAE=∠G

∵E是CD的中点

∴DE=CE

∴△ADE≌△GCE

∴AD=CG

∵AD=DC=4

∴CG=4，CE=2

在Rt△GCE中，

∴GE=

（2）

证明：由（1）得：△ADE≌△GCE

∴AE=GE

∵∠AEF=90°

∴EF垂直平分AG

∴AF=GF

∴∠FAE=∠G

∵∠DAE=∠G

∴∠FAE=∠DAE

∴AE平分∠DAF

（3）

解：在正方形ABCD中

∠B=∠BCD=∠D=90°，AB=BC=CD=DA=4

∴DE=CE=2

设CF=x，则BF=4-x

根据勾股定理得：

AF2=AB2+ BF2=42+(4-x)2=32-8x+x2

EF2=CF2+ CE2=x2+22= x2+4

AE2=AD2+ DE2=42+22=20

在Rt△AEF中，AF2= EF2+ AE2

∴32-8x+ x2= x2+4+20

解得:x=1

∴CF=1

【解析】（1）由正方形的性质可以得到△ADE≌△GCE（AAS）,根据全等三角形的性质可以得AD=CG；在Rt△GCE中，由勾股定理得到GE长。
（2）由（1）得：△ADE≌△GCE，根据全等三角形的性质可以得AE=GE；再∠AEF=90°，由等腰三角形的性质三线合一可以得到EF垂直平分AG，
AF=GF；再根据等边对等角得∠FAE=∠G，由等量代换可以∠FAE=∠DAE；即AE平分∠DAF。
（3）设CF=x，则BF=4-x，由勾股定理得：AF2=AB2+ BF2=42+(4-x)2=32-8x+x2；EF2=CF2+ CE2=x2+22= x2+4；AE2=AD2+ DE2=42+22=20；
在Rt△AEF中，由AF2= EF2+ AE2解得x=1，即CF=1
【考点精析】根据题目的已知条件，利用角的平分线和等腰三角形的性质的相关知识可以得到问题的答案，需要掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；等腰三角形的两个底角相等（简称：等边对等角）．