
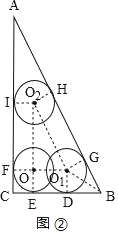
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=7+2![]() ,圆形纸片的半径为2,求圆心O运动的路径长为_____.
,圆形纸片的半径为2,求圆心O运动的路径长为_____.

【答案】15+5![]() .
.
【解析】
添加如图所示辅助线,圆心O的运动路径长为![]() ,先求出△ABC的三边长度,得出其周长,证四边形OEDO1、四边形O1O2HG、四边形OO2IF均为矩形、四边形OECF为正方形,得出∠OO1O2=60°=∠ABC、∠O1OO2=90°,从而知△OO1O2∽△CBA,利用相似三角形的性质即可得出答案.
,先求出△ABC的三边长度,得出其周长,证四边形OEDO1、四边形O1O2HG、四边形OO2IF均为矩形、四边形OECF为正方形,得出∠OO1O2=60°=∠ABC、∠O1OO2=90°,从而知△OO1O2∽△CBA,利用相似三角形的性质即可得出答案.
如图,圆心O的运动路径长为![]() ,
,
过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB,垂足分别为点D、F、G,
过点O作OE⊥BC,垂足为点E,
过点O2作O2H⊥AB,O2I⊥AC,垂足分别为点H、I,
在Rt△ABC中,∠ACB=90°、∠A=30°,
∴AC=![]() =7
=7![]() +6,AB=2BC=14+4
+6,AB=2BC=14+4![]() ,∠ABC=60°,
,∠ABC=60°,
∴C△ABC=13![]() +27,
+27,
∵O1D⊥BC、O1G⊥AB,
∴D、G为切点,
∴BD=BG,
在Rt△O1BD和Rt△O1BG中,
∵![]() ,
,
∴△O1BD≌△O1BG(HL),
∴∠O1BG=∠O1BD=30°,
在Rt△O1BD中,∠O1DB=90°,∠O1BD=30°,
∴BD=![]() =2
=2![]() ,
,
∴OO1=7+2![]() ﹣2﹣2
﹣2﹣2![]() =5,
=5,
∵O1D=OE=2,O1D⊥BC,OE⊥BC,
∴O1D∥OE,且O1D=OE,
∴四边形OEDO1为平行四边形,
∵∠OED=90°,
∴四边形OEDO1为矩形,
同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,
又OE=OF,
∴四边形OECF为正方形,
∵∠O1GH=∠CDO1=90°,∠ABC=60°,
∴∠GO1D=120°,
又∵∠FO1D=∠O2O1G=90°,
∴∠OO1O2=360°﹣90°﹣90°=60°=∠ABC,
同理,∠O1OO2=90°,
∴△OO1O2∽△CBA,
∴![]() ,即
,即![]() ,
,
∴C△OO1O2=15+5![]() ,
,
即圆心O运动的路径长为15+5![]() .
.
故答案为15+5![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿线段CA以每秒2cm的速度运动,同时点Q从点B出发沿线段BC以每秒1cm的速度运动.设运动时间为t秒(0<t<5).
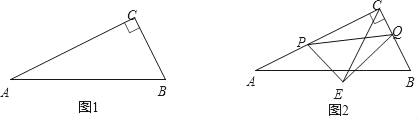
(1)填空:AB= cm;
(2)t为何值时,△PCQ与△ACB相似;
(3)如图2,以PQ为斜边在异于点C的一侧作Rt△PEQ,且![]() ,连结CE,求CE.(用t的代数式表示).
,连结CE,求CE.(用t的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
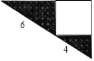
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
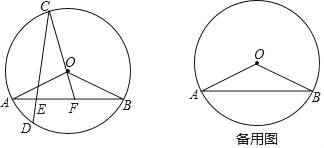
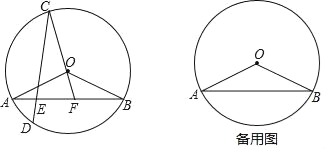
【题目】如图,在⊙O中,弦AB、CD相交于点E,![]() =
=![]() ,点D在
,点D在![]() 上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=
上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=![]() ,tan∠OBA=
,tan∠OBA=![]() .
.
(1)求证:∠OBA=∠OCD;
(2)当△AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求EF的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB、CD相交于点E,![]() =
=![]() ,点D在
,点D在![]() 上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=
上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=![]() ,tan∠OBA=
,tan∠OBA=![]() .
.
(1)求证:∠OBA=∠OCD;
(2)当△AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求EF的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).①如图1,若BC=4m,则S= m2.②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变则在BC的变化过程中,当S取得最小值时,边BC的长为 m.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com