
【题目】如图,点A(m,4),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=3,在x轴上存在一点P,使|PA﹣PB|的值最大,则P点的坐标是( )
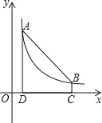
A. (5,0)B. (4.0)C. (3,0)D. (2,0)
【答案】A
【解析】
根据题意列出关于m、n的方程组,得到m、n的值,求出反比例函数解析式,由三角形三边关系可知,当A、B、P在同一条直线上时,|PA﹣PB|最大,求出直线AB的解析式,即可得到P点坐标.
设反比例函数的表达式为y=![]() ,
,
∵A(m,4),B(n,1)在反比例函数上,
∴4m=n,
∵DC=3,
∴n﹣m=3,
解得:m=1,n=4,
∴A(1,4),B(4,1)
把A(1,4)代入y=![]() 中,
中,
解得:k=4
∴反比例函数表达式为y=![]() .
.
由三角形三边关系,两边之差小于第三边可得,|PA﹣PB|<AB,
所以当A、B、P在同一条直线上时,PA﹣PB=AB时,|PA﹣PB|最大.
设直线AB的解析式为y=kx+b
将A(1,4),B(4,1)代入解析式可得:k=﹣1,b=5
所以直线AB的解析式为y=﹣x+5,
∵P在x轴上,当y=0时,x=5,
∴P(5,0).
故选:A.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
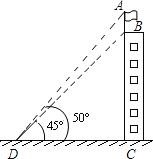
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产一种饮料是由A,B两种原料液按一定比例配制而成,其中A原料液的成本价为15元/千克,B原料液的成本价为10元/千克,按现行价格销售每千克获得70%的利润率.由于市场竞争,物价上涨,A原料液上涨20%,B原料液上涨10%,配制后的总成本增加了12%,公司为了拓展市场,打算再投入现总成本的25%做广告宣传,如果要保证每千克利润不变,则此时这种饮料的利润率是
查看答案和解析>>
科目:初中数学 来源: 题型:
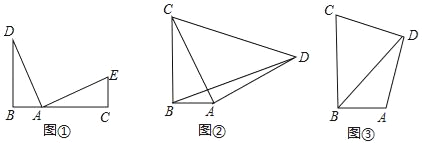
【题目】(1)观察猜想
如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为;
(2)问题解决
如图②,在Rt△ABC中,∠ABC=90°,CB=4,AB=2,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;
(3)拓展延伸
如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=4,AB=2,DC=DA,请直接写出BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
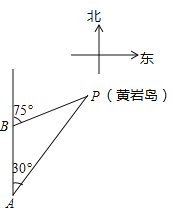
【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据: ![]() ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得正方形A1B1C1D1,且剩下图形的面积为原正方形面积的![]() ,则AA1=_____.
,则AA1=_____.
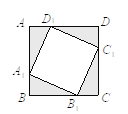
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是菱形,边BC在x轴上,点A(0,4),点B(3,0),双曲线y=![]() 与直线BD交于点D、点E.
与直线BD交于点D、点E.
(1)求k的值;
(2)求直线BD的解析式;
(3)求△CDE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com