
ЁОЬтФПЁПЖЈвхЃКдкЦНУцжБНЧзјБъЯЕжаЃЌНЋЕуPШЦЕуTЃЈtЃЌ0ЃЉЃЈtЃО0ЃЉа§зЊ180ЁуЕУЕНЕуQЃЌдђГЦЕуQЮЊЕуPЕФЁАЗЂеЙЕуЁБЃЎ
ЃЈ1ЃЉЕБtЃН3ЪБЃЌЕуЃЈ0ЃЌ0ЃЉЕФЁАЗЂеЙЕуЁБзјБъЮЊЁЁ ЁЁЃЌЕуЃЈЉ1ЃЌЉ1ЃЉЕФЁАЗЂеЙЕуЁБзјБъЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉШєtЃО2ЃЌдђЕуЃЈ2ЃЌ3ЃЉЕФЁАЗЂеЙЕуЁБЕФКсзјБъЮЊЁЁ ЁЁЃЈгУКЌtЕФДњЪ§ЪНБэЪО ЃЉЃЎ
ЃЈ3ЃЉШєЕуPдкжБЯпyЃН2x+6ЩЯЃЌЦфЁАЗЂеЙЕуЁБQдкжБЯпyЃН2xЉ8ЩЯЃЌЧѓЕуTЕФзјБъЃЎ
ЃЈ4ЃЉЕуPЃЈ2ЃЌ2ЃЉдкХзЮяЯпyЃНЉx2+kЩЯЃЌЕуMдкетЬѕХзЮяЯпЩЯЃЌЕуQЮЊЕуPЕФЁАЗЂеЙЕуЁБЃЌШєЁїPMQЪЧвдЕуMЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ6ЃЌ0ЃЉЃЌЃЈ7ЃЌ1ЃЉЃЛЃЈ2ЃЉ2tЉ2ЃЛЃЈ3ЃЉTЃЈ![]() ЃЌ0ЃЉЃЛЃЈ4ЃЉtЕФжЕЮЊ
ЃЌ0ЃЉЃЛЃЈ4ЃЉtЕФжЕЮЊ![]() Лђ5ЃЎ
Лђ5ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЪ§аЮНсКЯЕФЫМЯыКЭжааФЖдГЦЕФаджЪЧѓНтЃЛ
ЃЈ2ЃЉРћгУЪ§аЮНсКЯЕФЫМЯыКЭжааФЖдГЦЕФаджЪЧѓНтЃЛ
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕуКЭ
ЕуКЭ![]() ЕуЙигк
ЕуЙигк![]() ЖдГЦЃЌИљОнжаЕузјБъЙЋЪНЕУЕН
ЖдГЦЃЌИљОнжаЕузјБъЙЋЪНЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌШЛКѓЧѓГі
ЃЌШЛКѓЧѓГі![]() ЕУЕН
ЕУЕН![]() ЕузјБъЃЛ
ЕузјБъЃЛ
ЃЈ4ЃЉЯШАб![]() ДњШы
ДњШы![]() жаЧѓГі
жаЧѓГі![]() ЕУЕНХзЮяЯпНтЮіЪНЮЊ
ЕУЕНХзЮяЯпНтЮіЪНЮЊ![]() ЃЌРћгУЕу
ЃЌРћгУЕу![]() ЮЊЕу
ЮЊЕу![]() ЕФЁАЗЂеЙЕуЁБЕУЕНЕу
ЕФЁАЗЂеЙЕуЁБЕУЕНЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌдйИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕН
ЕФжаЕуЃЌдйИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕН![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌЬжТлЃКЕБ
ЮЊЕШбќжБНЧШ§НЧаЮЃЌЬжТлЃКЕБ![]() ЪБЃЌАб
ЪБЃЌАб![]() ЕуШЦ
ЕуШЦ![]() ЕуЫГЪБеыа§зЊ
ЕуЫГЪБеыа§зЊ![]() ЕУЕНЕу
ЕУЕНЕу![]() ЃЌРћгУа§зЊЕФаджЪвзЕУ
ЃЌРћгУа§зЊЕФаджЪвзЕУ![]() ЃЌШЛКѓ
ЃЌШЛКѓ![]() ЕуЕФзјБъДњШы
ЕуЕФзјБъДњШы![]() ЕУ
ЕУ![]() ЃЌдйНтЗНГЬМДПЩЃЛЕБ
ЃЌдйНтЗНГЬМДПЩЃЛЕБ![]() ЪБЃЌРћгУЭЌбљЗНЗЈЧѓЖдгІ
ЪБЃЌРћгУЭЌбљЗНЗЈЧѓЖдгІ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ1ЃЉАбЃЈ0ЃЌ0ЃЉШЦЕуЃЈ3ЃЌ0ЃЉа§зЊ180ЁуЕУЕНЕуЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЛ
АбЃЈЉ1ЃЌЉ1ЃЉШЦЕуЃЈ3ЃЌ0ЃЉа§зЊ180ЁуЕУЕНЕуЕФзјБъЮЊЃЈ7ЃЌ1ЃЉЃЛ
ЃЈ2ЃЉАбЃЈ2ЃЌ3ЃЉШЦЕуЃЈtЃЌ0ЃЉа§зЊ180ЁуЕУЕНЕуЕФзјБъЮЊЃЈ2tЉ2ЃЌЉ3ЃЉЃЛ
ЙЪД№АИЮЊЃЈ6ЃЌ1ЃЉЃЌЃЈ7ЃЌ1ЃЉЃЛ2tЉ2ЃЛ
ЃЈ3ЃЉЩшPЃЈmЃЌ2m+6ЃЉЃЌQЃЈnЃЌ2nЉ8ЃЉЃЌ
ЁпPЕуКЭQЕуЙигкTЃЈtЃЌ0ЃЉЖдГЦЃЌ
Ёр![]() ЃН0ЃЌ
ЃН0ЃЌ![]() ЃНtЃЌ
ЃНtЃЌ
Ёрm+nЃН1ЃЌtЃН![]() ЃЌ
ЃЌ
ЁрTЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЃЈ4ЃЉАбЃЈ2ЃЌ2ЃЉДњШыyЃНЉx2+kЕУЉ4+kЃН2ЃЌ
НтЕУkЃН6ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊyЃНЉx2+6ЃЌ
ЁпЕуQЮЊЕуPЕФЁАЗЂеЙЕуЁБЃЌ
ЁрЕуTЮЊPQЕФжаЕуЃЌ
ЁпЁїPMQЪЧвдЕуMЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌ
ЁрMTДЙжБЦНЗжPQЃЌ
ЁрЁїPTMЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЕБ0ЃМtЁм2ЪБЃЌ
АбPЕуШЦTЕуЫГЪБеыа§зЊ90ЁуЕУЕНЕуMЃЌ
дђMЃЈt+2ЃЌtЉ2ЃЉЃЌ
АбMЃЈt+2ЃЌtЉ2ЃЉДњШыyЃНЉx2+6ЕУЉЃЈt+2ЃЉ2+6ЃНtЉ2ЃЌ
НтЕУt1ЃН![]() ЃЌt2ЃН
ЃЌt2ЃН![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЕБtЃО2ЪБЃЌ
АбPЕуШЦTЕуФцЪБеыа§зЊ90ЁуЕУЕНЕуMЃЌ
дђMЃЈtЉ2ЃЌ2ЉtЃЉЃЌ
АбMЃЈtЉ2ЃЌ2ЉtЃЉДњШыyЃНЉx2+6ЕУЉЃЈtЉ2ЃЉ2+6ЃН2ЉtЃЌ
НтЕУt1ЃН5ЃЌt2ЃН0ЃЈЩсШЅЃЉЃЌ
злЩЯЫљЪіЃЌtЕФжЕЮЊ![]() Лђ5ЃЎ
Лђ5ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГЛѕеОДЋЫЭЛѕЮяЕФЦНУцЪОвтЭМЃЌADгыЕиУцЕФМаНЧЮЊ60ЁуЃЌЮЊСЫЬсИпДЋЫЭЙ§ГЬЕФАВШЋадЃЌЙЄШЫЪІИЕгћМѕаЁДЋЫЭДјгыЕиУцЕФМаНЧЃЌЪЙЦфгЩ45ЁуБфГЩ37ЁуЃЌвђДЫДЋЫЭДјЕФТфЕиЕугЩЕуBЕНЕуCЯђЧАвЦЖЏСЫ2Уз.

ЃЈ1ЃЉЧѓЕуAгыЕиУцЕФИпЖШЃЛ
ЃЈ2ЃЉШчЙћашвЊдкЛѕЮязХЕиЕуCЕФзѓВрСєГі2УзЃЌФЧУДЧыХаЖЯОрРыDЕу14УзЕФЛѕЮя2ЪЧЗёашвЊХВзпЃЌВЂЫЕУїРэгЩ.ЃЈsin37ЁуЁж0.6ЃЌcos37ЁуЁж0.8ЃЌtan37ЁуЁж0.75ЃЌ![]() Ёж1.73ЃЉ
Ёж1.73ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжгФЯЩНдКЪПЬИЕНЗРЛЄаТаЭЙкзДВЁЖОЗЮбзЪБЫЕЃКЁАЮвУЧашвЊжиЪгЗРЛЄЃЌЕЋвВВЛБиПжЛХЃЌОЁСПЩйШЅШЫдБУмМЏЕФГЁЫљЃЌГіУХДїПкежЃЌдкЪвФкзЂвтЭЈЗчЃЌЧкЯДЪжЃЌЖрдЫЖЏЃЌЩйАОвЙЃЎЁБЁФГЩчЧјЮЊСЫМгЧПЩчЧјОгУёЖдаТаЭЙкзДВЁЖОЗЮбзЗРЛЄжЊЪЖЕФСЫНтЃЌЭЈЙ§ЮЂаХШКаћДЋаТаЭЙкзДВЁЖОЗЮбзЕФЗРЛЄжЊЪЖЃЌВЂЙФРјЩчЧјОгУёдкЯпВЮгызїД№ЁЖ2020ФъаТаЭЙкзДВЁЖОЗРжЮШЋЙњЭГвЛПМЪдЃЈШЋЙњОэЃЉЁЗЪдОэЃЌЩчЧјЙмРэдБЫцЛњДгМзЁЂввСНИіаЁЧјИїГщШЁ20УћШЫдБЕФД№ОэГЩМЈЃЌВЂЖдЫћУЧЕФГЩМЈЃЈЕЅЮЛЃКЗжЃЉНјааЭГМЦЁЂЗжЮіЃЌЙ§ГЬШчЯТЃК
ЪеМЏЪ§ОнЃК
МзаЁЧјЃК | 85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 | 90 | 90 | 70 |
90 | 100 | 80 | 80 | 90 | 95 | 75 | |||||||
вваЁЧјЃК | 80 | 60 | 80 | 95 | 65 | 100 | 90 | 85 | 85 | 80 | 95 | 75 | 80 |
90 | 70 | 80 | 95 | 75 | 100 | 90 |
ећРэЪ§ОнЃК
ГЩМЈ xЃЈЗжЃЉ | 60ЁмxЁм70 | 70ЃМxЁм80 | 80ЃМxЁм90 | 90ЃМxЁм100 |
МзаЁЧј | 2 | 5 | a | b |
вваЁЧј | 3 | 7 | 5 | 5 |
ЗжЮіЪ§ОнЃК
ЭГМЦСП | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ |
МзаЁЧј | 85.75 | 87.5 | c |
вваЁЧј | 83.5 | d | 80 |
гІгУЪ§ОнЃК
ЃЈ1ЃЉЬюПеЃК![]() ЃН ЃЌ
ЃН ЃЌ![]() ЃН ЃЌ
ЃН ЃЌ![]() ЃН ЃЌ
ЃН ЃЌ![]() ЃН ЃЛ
ЃН ЃЛ
ЃЈ2ЃЉШєМзаЁЧјЙВга800ШЫВЮгыД№ОэЃЌЧыЙРМЦМзаЁЧјГЩМЈДѓгк90ЗжЕФШЫЪ§ЃЛ
ЃЈ3ЃЉЩчЧјЙмРэдБПДЭъЭГМЦЪ§ОнЃЌзМБИДгГЩМЈдк60ЕН70ЗжжЎМфЕФСНИіаЁЧјжаЫцЛњГщШЁ2ШЫНјаадйВтЪдЃЌЧыЧѓГіГщШЁЕФСНШЫЧЁКУвЛИіЪЧМзаЁЧјЁЂвЛИіЪЧвваЁЧјЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШчЭМ1ЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЁЂ
ЁЂ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЮвУЧАбетжжФЃаЭГЦЮЊЁААыНЧФЃаЭЁБЃЌдкНтОіЁААыНЧФЃаЭЁБЮЪЬтЪБЃЌа§зЊЪЧвЛжжГЃгУЕФЗНЗЈЃЎ
ЃЌЮвУЧАбетжжФЃаЭГЦЮЊЁААыНЧФЃаЭЁБЃЌдкНтОіЁААыНЧФЃаЭЁБЮЪЬтЪБЃЌа§зЊЪЧвЛжжГЃгУЕФЗНЗЈЃЎ
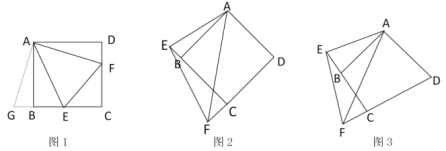
ЃЈ1ЃЉдкЭМlжаЃЌСЌНг![]() ЃЌЮЊСЫжЄУїНсТлЁА
ЃЌЮЊСЫжЄУїНсТлЁА![]() ЁБЃЌаЁССНЋ
ЁБЃЌаЁССНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() КѓНтД№СЫетИіЮЪЬтЃЌЧыАДаЁССЕФЫМТЗаДГіжЄУїЙ§ГЬЃЛ
КѓНтД№СЫетИіЮЪЬтЃЌЧыАДаЁССЕФЫМТЗаДГіжЄУїЙ§ГЬЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() ШЦЕу
ШЦЕу![]() а§зЊЕНЭМ2ЮЛжУЪБЃЌЪдЬНОП
а§зЊЕНЭМ2ЮЛжУЪБЃЌЪдЬНОП![]() гы
гы![]() ЁЂ
ЁЂ![]() жЎМфгадѕбљЕФЪ§СПЙиЯЕЃП
жЎМфгадѕбљЕФЪ§СПЙиЯЕЃП
ЃЈ3ЃЉШчЭМ3ЃЌШчЙћЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЁШ§еХаЮзДДѓаЁвЛбљЃЌжЪЕиЭъШЋЕФЯрЭЌПЈЦЌЃЌдкШ§еХПЈЦЌЩЯЗжБ№аДЩЯЁАРюУїЁЂЭѕЧПЁЂЫяЮАЁБетШ§ИіЭЌбЇЕФУћзжЃЌШЛКѓНЋШ§еХПЈЦЌЗХШывЛИіВЛЭИУїЕФКазгРяЃЎ
ЃЈ1ЃЉСжРЯЪІДгКазгжаШЮШЁвЛеХЃЌЧѓШЁЕНаДгаРюУїУћзжЕФПЈЦЌИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉСжРЯЪІДгКазгжаШЁГівЛеХПЈЦЌЃЌМЧЯТУћзжКѓЗХЛиЃЌдйДгКазгжаШЁГіЕкЖўеХПЈЦЌЃЌМЧЯТУћзжЃЎгУСаБэЛђЛЪїаЮЭМСаГіСжРЯЪІШЁЕНЕФПЈЦЌЕФЫљгаПЩФмЧщПіЃЌВЂЧѓГіСНДЮЖМШЁЕНаДгаРюУїУћзжЕФПЈЦЌЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮ![]() ЖЅЕу
ЖЅЕу![]() дкКЏЪ§
дкКЏЪ§![]()
![]() ЕФЭМЯѓЩЯЃЌКЏЪ§
ЕФЭМЯѓЩЯЃЌКЏЪ§![]()
![]() ЕФЭМЯѓЙигкжБЯп
ЕФЭМЯѓЙигкжБЯп![]() ЖдГЦЃЌЧвОЙ§Еу
ЖдГЦЃЌЧвОЙ§Еу![]() ЃЌ
ЃЌ![]() СНЕуЃЌШє
СНЕуЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊ________ЃЎ
ЕФжЕЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкзјБъЦНУцФкЃЌЁїABCЕФЖЅЕуЮЛжУШчЭМЫљЪОЃЎ
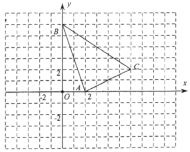
ЃЈ1ЃЉНЋЁїABCзїЦНвЦНЛЛЛЃЈxЃЌyЃЉЁњЃЈx+2ЃЌy-3ЃЉЕУЕН![]() ЃЌЛГі
ЃЌЛГі![]() ЃЎ
ЃЎ
ЃЈ2ЃЉвдЕуOЮЊЮЛЫЦжааФЫѕаЁ![]() ЕУЕН
ЕУЕН![]() ЃЌЪЙ
ЃЌЪЙ![]() гы
гы![]() ЕФЯрЫЦБШЮЊ1ЃК2ЃЌЧвЕуAгыЦфЖдгІЕу
ЕФЯрЫЦБШЮЊ1ЃК2ЃЌЧвЕуAгыЦфЖдгІЕу![]() ЮЛгкЕуOЕФСНВрЃЌЛГі
ЮЛгкЕуOЕФСНВрЃЌЛГі![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
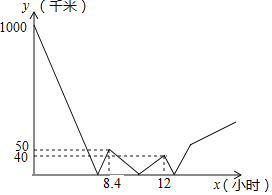
ЁОЬтФПЁПдкЭЌвЛжБЯпЩЯгаAЁЂBСНЕиЃЌМзГЕДгAЕиЫЭЛѕЕНBЕиЃЌЭЌЪБввГЕДгBЕиЧАЭљAЕиЃЌСНГЕНддШЫйааЪЛЃЎЭОжаФГвЛЪБПЬЃЌМзГЕЗЂЯжгаЛѕЮяТфдкAЁЂBжЎМфЕФФГДІCЕиЃЌгкЪЧСЂПЬЕєЭЗВЂвдздМКдРДЫйЖШЕФСНБЖдШЫйЗЕЛиЃЌШЁЕНЛѕЮяКѓЃЌдйвдзюГѕЕФЫйЖШМЬајдШЫйЯђBЕиааЪЛЃЎСНГЕжЎМфЕФОрРыyЃЈЧЇУзЃЉгыМзГЕааЪЛЕФЪБМфxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЈЭОжаЕєЭЗЁЂШЁЛѕЮяЕЂЮѓЪБМфКіТдВЛМЦЃЉЃЌЕБввГЕЕНДяAЕиЪБЃЌМзГЕЕНAЕиЕФОрРыЮЊ_____ЧЇУзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙњМвЙцЖЈЃЌжааЁбЇЩњУПЬьдкаЃЬхг§ЛюЖЏЪБМфВЛЕЭгк1аЁЪБЃЎЮЊСЫНтетЯюеўВпЕФТфЪЕЧщПіЃЌгаЙиВПУХОЭЁАФуФГЬьдкаЃЬхг§ЛюЖЏЪБМфЪЧЖрЩйЁБЕФЮЪЬтЃЌдкФГаЃЫцЛњГщВщСЫВПЗжбЇЩњЃЌдйИљОнЛюЖЏЪБМф![]() ЃЈаЁЪБЃЉНјааЗжзщЃЈAзщЃК
ЃЈаЁЪБЃЉНјааЗжзщЃЈAзщЃК![]() ЃЌBзщЃК
ЃЌBзщЃК![]() ЃЌCзщЃК
ЃЌCзщЃК![]() ЃЌDзщЃК
ЃЌDзщЃК![]() ЃЉЃЌЛцжЦГЩШчЯТСНЗљЭГМЦЭМЃЌЧыИљОнЭМжааХЯЂЛиД№ЮЪЬтЃК
ЃЉЃЌЛцжЦГЩШчЯТСНЗљЭГМЦЭМЃЌЧыИљОнЭМжааХЯЂЛиД№ЮЪЬтЃК
ЃЈ1ЃЉДЫДЮГщВщЕФбЇЩњЪ§ЮЊ________ШЫЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ

ЃЈ3ЃЉДгГщВщЕФбЇЩњжаЫцЛњбЏЮЪвЛУћбЇЩњЃЌИУЩњЕБЬьдкаЃЬхг§ЛюЖЏЪБМфЕЭгк1аЁЪБЕФИХТЪЪЧ__________ЃЛ
ЃЈ4ЃЉШєЕБЬьдкаЃбЇЩњЪ§ЮЊ1200ШЫЃЌЧыЙРМЦдкЕБЬьДяЕНЙњМвЙцЖЈЬхг§ЛюЖЏЪБМфЕФбЇЩњга__________ШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com