练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在坐标平面内，△ABC的顶点位置如图所示．

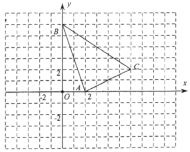
    （1）将△ABC作平移交换（x，y）→（x+2，y-3）得到，画出．

    （2）以点O为位似中心缩小得到，使与的相似比为1：2，且点A与其对应点位于点O的两侧，画出．

    【答案】（1）见解析 （2）见解析

    【解析】

    （1）根据△ABC作平移交换（x，y）→（x+2，y-3），得出平移方向和距离，据此作出三顶点平移后的对应点，顺次连接可得；

    （2）利用已知坐标系得出将△ABC作位似变换且缩小为原来的，即对应点坐标乘以，

    据此作出三顶点平移后的对应点，顺次连接可得.

    （1）由题意知，△ABC先向右平移2个单位、再向下平移3个单位可以得到作图如下：

    （2）将△ABC以点O为位似中心作位似变换且缩小为原来的，且点A与其对应点位于点O的两侧，作图如下：

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在某次商业足球比赛中，门票销售单位对团体购买门票实行优惠，决定在原定票价基础上每张降价100元，这样按原定票价需花费14 000元购买的门票张数，现在只花费了10 500元．

    (1)求每张门票的原定票价；

    (2)根据实际情况，组织单位决定对于个人购票也采取优惠措施，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020贺岁片《囧妈》提档大年三十网络首播.“乐调查”平台为了全面了解观众对《囧妈》的满意度情况，进行随机抽样调查，分为四个类别：.非常满意；.满意；.基本满意；.不满意，依据调查数据绘制成图1和图2的统计图（不完整）．

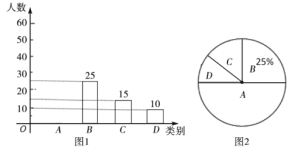
    根据以上信息，解答下列问题：

    （1）本次接受调查的观众共有_______人；

    （2）扇形统计图中，扇形的圆心角度数是_______；

    （3）请补全条形统计图；

    （4）“乐调查”平台调查了春节期间观看《固妈》的观众约5000人，请估计观众对该电影的满意（、、类视为满意）的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：在平面直角坐标系中，将点P绕点T（t，0）（t＞0）旋转180°得到点Q，则称点Q为点P的“发展点”．

    （1）当t＝3时，点（0，0）的“发展点”坐标为　 　，点（﹣1，﹣1）的“发展点”坐标为　 　．

    （2）若t＞2，则点（2，3）的“发展点”的横坐标为　 　（用含t的代数式表示 ）．

    （3）若点P在直线y＝2x+6上，其“发展点”Q在直线y＝2x﹣8上，求点T的坐标．

    （4）点P（2，2）在抛物线y＝﹣x2+k上，点M在这条抛物线上，点Q为点P的“发展点”，若△PMQ是以点M为直角顶点的等腰直角三角形，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：给定一个矩形，如果存在另一个矩形，它的周长和面积分别是已知矩形的周长和面积的一半，则这个矩形是给定矩形的“减半”矩形．如图，矩形是矩形的“减半”矩形．

    请你解决下列问题：

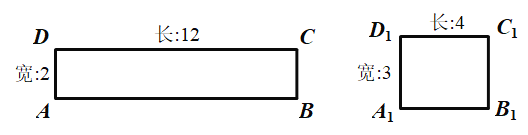
    （1）当矩形的长和宽分别为，时，它是否存在“减半”矩形？请作出判断，并说明理由．

    （2）边长为的正方形存在“减半”正方形吗？如果存在，求出“减半”正方形的边长；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

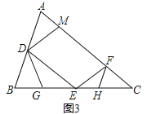
    【题目】如图1，锐角△ABC中，D、E分别是AB、BC的中点，F是AC上的点，且∠AFE=∠A，DM//EF交AC于点M．

    （1）求证：DM=DA；

    （2）点G在BE上，且∠BDG=∠C，如图2，

    ① 求证：△DEG∽△ECF；

    ② 从线段CE上取一点H，连接FH使∠CFH=∠B，若BG=1，求EH的长．

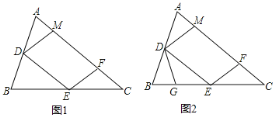
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，△ABC中AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于G，交AB于点F，FB恰为⊙O的直径．

    （1）求证：AE与⊙O相切；

    （2）当BC=6，cosC=，求⊙O的直径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校今年组织学生参加志愿者活动，活动分为甲、乙、丙三组进行．下面的条形统计图和扇形统计图反映了学生参加活动的报名情况，请你根据图中的信息，解答下列问题：

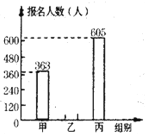
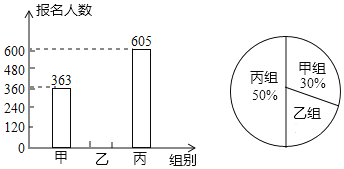
    （1）若在参加活动的学生中随机抽取一名学生，则抽到乙组学生的概率是

    （2）今年参加志愿者共 人，并把条形统计图补充完整；

    （3）学校两年前参加志愿者的总人数是810人，若这两年的年增长率相同，求这个年增长率．（精确到1%）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

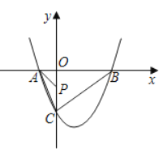
    【题目】如图，已知二次函数的图象交轴于，两点，交轴于点，其中.

    （1）求点的坐标，并用含的式子表示；

    （2）连接，，当为锐角时，求的取值范围；

    （3）若为轴上一个动点，连接，当点的坐标为时，直接写出的最小值．

    查看答案和解析>>

    同步练习册答案