
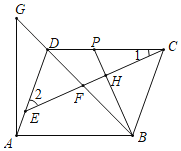
【题目】在平行四边形ABCD中,点E是AD边上一点,连接CE,交对角线BD于点F,过点A作AB的垂线交BD的延长线于点G,过B作BH垂直于CE,垂足为点H,交CD于点P,2∠1+∠2=90°.
(1)若PH=2,BH=4,求PC的长;
(2)若BC=FC,求证:GF=![]() PC.
PC.
【答案】(1)2![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据四边形ABCD是平行四边形,先证∠BCP=∠BPC,再根据勾股定理即可求出答案;
(2)由(1)得:BC=BP=AD,可知四边形ABPD是等腰梯形,从而证∠1=∠GAD,然后证△DAG≌△FCD,作FM⊥CD于M,BN⊥CD于N,△CFM≌△BPN即可求出答案.
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB∥CD,AB=CD,
∴∠BCH=∠2,
∴∠BCP=∠2+∠1,
∵2∠1+∠2=90°.
∴∠BCP=90°﹣∠1,
∵BH⊥CE,
∴∠BPC+∠1=90°,
∴∠BPC=90°﹣∠1,
∴∠BCP=∠BPC,
∴BC=BP=BH+PH=4+2=6,
∴CH2=BC2﹣BH2=62﹣42=20,
∴PC=![]() =
=![]() =2
=2![]() ;
;
(2)证明:由(1)得:BC=BP=AD,
∴四边形ABPD是等腰梯形,
∴∠DAB=∠PBA,
∵CD∥AB,
∴∠PBA=∠BPC,
∵BH⊥CE,
∴∠1=90°﹣∠BPC=90°﹣∠PBA=90°﹣∠DAB=∠GAD,
∵AD=BC,BC=FC,
∴AD=FC,∠CBF=∠CFB,
∵AD∥BC,
∴∠EDF=∠CBF,
∴∠EDF=∠CFB=∠EFD,
∴∠ADG=∠CFD,
在△DAG和△FCD中,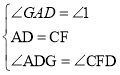 ,
,
∴△DAG≌△FCD(ASA),
∴AG=CD=AB,DG=FD,
∵AG⊥AB,
∴△ABG是等腰直角三角形,
∴∠DBA=∠G=45°,
作FM⊥CD于M,BN⊥CD于N,如图所示:
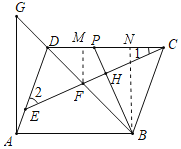
∵AB∥CD,
∴∠CDF=∠DBA=45°,
∴△DMF是等腰直角三角形,
∴DM=FM,DF=![]() FM,
FM,
∵BN⊥CD,BH⊥CE,
∴由三角形内角和定理得:∠1=∠PBN,
在△CFM和△BPN中, ,
,
∴△CFM≌△BPN(AAS),
∴FM=PN,
∵BC=BP,BN⊥CD,
∴PN=CN,
∴PC=2PN=2FM=![]() DF,
DF,
∴![]() PC=2DF,
PC=2DF,
∴GF=2DF=![]() PC
PC


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .请按照要求写出符合条件的抛物线的解析式.
.请按照要求写出符合条件的抛物线的解析式.
(1)若抛物线![]() 与
与![]() 关于
关于![]() 轴对称,则
轴对称,则![]() = ;
= ;
(2)若抛物线![]() 与
与![]() 关于
关于![]() 轴对称,则
轴对称,则![]() = ;
= ;
(3)若抛物线![]() 与
与![]() 关于坐标原点对称,则
关于坐标原点对称,则![]() = ;
= ;
(4)若抛物线![]() 是由
是由![]() 绕着点P(1,0)旋转180°后所得,则
绕着点P(1,0)旋转180°后所得,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ C=90°,AC=5,BC=12,D 是 BC 边的中点.
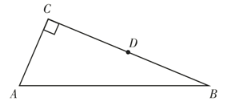
(1)尺规作图:过点 D 作 DE⊥AB 于点 E;(保留作图痕迹,不写做法)
(2)求 DE 的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 为
为![]() 的切线,切点分别为点
的切线,切点分别为点![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
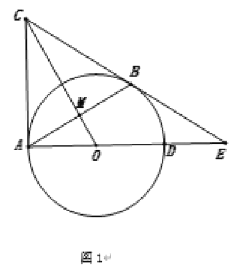
(1)如图1,求证:![]() ;
;
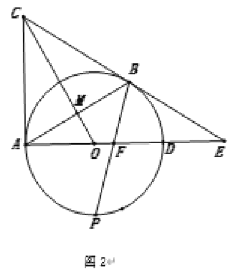
(2)如图2,点![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 交AD于点
交AD于点![]() ,求证:
,求证:![]() ;
;
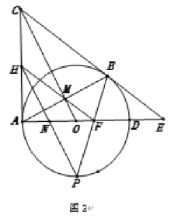
(3)如图3,在(2)的条件下:连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲投资销售一种利润率为0.4的电子产品,第一次购入的电子产品销售完后,甲取出28万元,并把剩下的本金和利润全部用于购入该电子产品;第二次购入的电子产品销售完后,再次取出19.6万元,并把剩下的本金和利润全部用于购入该电子产品;第三次购入电子产品销售完后,再次取出6.72万元.并把剩下的本金和利润全部用于购入该电子产品;第四次购入的电子产品销售完后,本次销售额为9.8万元,这样,甲投资该项目的本金和利润全部收回,则甲投资该项目的本金是_____万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列抛物线中,其顶点在反比例函数y=![]() 的图象上的是( )
的图象上的是( )
A.y=(x﹣4)2+3B.y=(x﹣4)2﹣3C.y=(x+2)2+1D.y=(x+2)2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com