
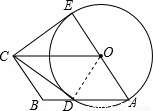
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.

(1)证明见解析;
(2)平行四边形OABC的面积S=12
【解析】
试题分析:(1)连接OD,求出∠EOC=∠DOC,根据SAS推出△EOC≌△DOC,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;
(2)根据全等三角形的性质求出CE=CD=4,根据平行四边形性质求出OA=3,根据平行四边形的面积公式求出即可.
试题解析:(1)连接OD,
∵OD=OA,
∴∠ODA=∠A,
∵四边形OABC是平行四边形,
∴OC∥AB,
∴∠EOC=∠A,∠COD=∠ODA,
∴∠EOC=∠DOC,
又∵OE=OD,OC=OC,
∴△EOC≌△DOC(SAS),
∴∠ODC=∠OEC=90°,
即OD⊥DC,
∴CD是⊙O的切线;
(2)∵△EOC≌△DOC,
∴CE=CD=4,
∵四边形OABC是平行四边形,
∴OA=BC=3,
∴平行四边形OABC的面积S=OA×CE=3×4=12.
考点:1、全等三角形的性质和判定;2、切线的判定与性质;3、平行四边形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:填空题
如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′= .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:解答题
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A.k> B.k≥
B.k≥ C.k>
C.k> 且k≠1 D.k≥
且k≠1 D.k≥ 且k≠1
且k≠1
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
一种微粒的半径是0.00004米,这个数据用科学记数法表示为( )
A.4×106 B.4×10﹣6 C.4×10﹣5 D.4×105
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:解答题
如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,
求证:△ABD≌△AEC.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
列方程或方程组解应用题:
小马自驾私家车从 地到
地到 地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动车所需电费27元,已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多
地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动车所需电费27元,已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多 元,求新购买的纯电动汽车每行驶1千米所需的电费.
元,求新购买的纯电动汽车每行驶1千米所需的电费.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:选择题
以下问题,不适合用全面调查的是( )
A.旅客上飞机前的安检
B.学校招聘教师,对应聘人员的面试
C.了解全校学生的课外读书时间
D.了解一批灯泡的使用寿命
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com