
��ͼ������ABC�У�D��BC���ϵĵ㣨�����B��C�غϣ�������AD��
�������룺
��1����ͼ��������D��BC���ϵ��е�ʱ��S��ABD��S��ABC=�� ��������D��BC��������һ��ʱ��S��ABD��S��ABC=�� ������ͼ�������߶α�ʾ����
̽���о���
��2����ͼ��������ABC�У�O�����߶�AD��һ�㣨�����A��D�غϣ�������BO��CO���Բ���S��BOC��S��ABC֮��Ӧ�õ���ͼ���������߶�֮�ȣ���˵�����ɣ�
��չӦ�ã�
��3����ͼ����O���߶�AD��һ�㣨�����A��D�غϣ�������BO���ӳ���AC�ڵ�F������CO���ӳ���AB�ڵ�E���Բ��� ��ֵ����˵�����ɣ�
��ֵ����˵�����ɣ�

��1��1��2��BD��BC��
��2��S��BOC��S��ABC=OD��AD�����ɼ�������
��3�� =1�����ɼ�������
=1�����ɼ�������
��������
�����������1�����������ε������ʽ���������εȸ�ʱ���ɵ��������ε�������Ĺ�ϵ���ɵô𰸣�
��2�����������ε������ʽ���������εȵ�ʱ���ɵ��������εĸ�������Ĺ�ϵ���ɵô𰸣�
��3�����������ε������ʽ���������εȵ�ʱ���ɵ��������εĸ�������Ĺ�ϵ���ٸ��ݷ�ʽ�ļӼ����ɵô���
�����������1����ͼ��������D��BC���ϵ��е�ʱ��S��ABD��S��ABC=1��2������D��BC��������һ��ʱ��S��ABD��S��ABC=BD��BC��
�ʴ�Ϊ��1��2��BD��BC��
��2��S��BOC��S��ABC=OD��AD��
��ͼ����OE��BC��E����AF��BC��F����
��OE��AF��
���OED�ס�AFD��
��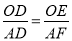 ��
��
�� ��
��
�� ��
��
��3�� =1���������£�
=1���������£�
�ɣ�2����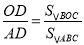 ��
�� ��
�� ��
��
�� =
= =
= =1��
=1��
 ��
��
���㣺�������ۺ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ�����������ѧ�������棩 ���ͣ�������
���㣺��25+�� ����1��|
����1��| ��8|+2cos60�㣮
��8|+2cos60�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��˱�������ѧ�������棩 ���ͣ�ѡ����
��������Ľ���У����������ǣ� ��
A������2014����1 B������2014����1
C������1��������2014�� D������2014����2014
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��ϳ������ѧ�������棩 ���ͣ�ѡ����
����� ��
�� ��
�� ��0��ͼ����ͼ��ʾ�����н��ۣ���
��0��ͼ����ͼ��ʾ�����н��ۣ��� ��0����
��0���� ��0���۵�
��0���۵� ��1ʱ��
��1ʱ�� ��
�� ����
���� ��0������
��0������ ��
�� ����
���� ��
�� ����
���� ��2��������ȷ���У�������
��2��������ȷ���У�������
A���٢ڢ� B���ڢ� C���ڢ� D���ڢۢ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��ϳ������ѧ�������棩 ���ͣ�ѡ����
���м����������ͼ�������ĶԳ�ͼ��������Գ�ͼ�ε��ǣ� ��




A B C D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��ڽ�������ѧ�������棩 ���ͣ������
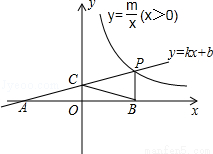
��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC=BC��
��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC=BC��
��1����һ�κ����������������Ľ���ʽ��
��2������������ͼ�����Ƿ���ڵ�D��ʹ�ı���BCPDΪ���Σ�������ڣ������D�����ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��ڽ�������ѧ�������棩 ���ͣ������
��ͼ�����ı���ABCD�У��Խ���AC��BD���ڵ�O��AD��BC��������һ���������� ����ʹ�ı���ABCDΪƽ���ı��Σ��������κθ����ߣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����־�����ѧ�������棩 ���ͣ������
��ͼ���ı���OABC��ƽ���ı��Σ���OΪԲ�ģ�OAΪ�뾶��Բ��AB��D���ӳ�AO����O��E������CD��CE����CE����O�����ߣ�����������⣺
��1����֤��CD����O�����ߣ�
��2����BC=3��CD=4����ƽ���ı���OABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�����������ѧ�������棩 ���ͣ�ѡ����
�ֶ���ij�������̻����м���Ϣ��һ��ʱ�䣮��֪�̻���� ����λ��ƽ���ף��빤��ʱ��
����λ��ƽ���ף��빤��ʱ�� ����λ��Сʱ���ĺ�����ϵ��ͼ����ͼ��ʾ������Ϣ���ֶ�ÿСʱ�̻����Ϊ
����λ��Сʱ���ĺ�����ϵ��ͼ����ͼ��ʾ������Ϣ���ֶ�ÿСʱ�̻����Ϊ

A��40ƽ���� B��50ƽ���� C��80ƽ���� D��100ƽ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com