
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ֱ��y=�� ![]() x+3��x�ᡢy��ֱ���A��B���㣬��P��Qͬʱ�ӵ�A�������˶�ʱ��Ϊt�룮���е�P������AB�˶����ٶ�Ϊÿ��4����λ���ȣ���Q������AO�˶����ٶ�Ϊÿ��5����λ���ȣ��Ե�QΪԲ�ģ�PQ��Ϊ�뾶����Q��
x+3��x�ᡢy��ֱ���A��B���㣬��P��Qͬʱ�ӵ�A�������˶�ʱ��Ϊt�룮���е�P������AB�˶����ٶ�Ϊÿ��4����λ���ȣ���Q������AO�˶����ٶ�Ϊÿ��5����λ���ȣ��Ե�QΪԲ�ģ�PQ��Ϊ�뾶����Q��
��1����֤��ֱ��AB�ǡ�Q�����ߣ�
��2������A���x���ϵ�����һ��C��m��0������ֱ��AB�Ĵ���CM������ΪM����CM���Q�����ڵ�D����m��t�ĺ�����ϵʽ������д���Ա�����ȡֵ��Χ����
��3���ڣ�2���������£��Ƿ���ڵ�C��ֱ��AB��CM��y�����Qͬʱ���У������ڣ���ֱ��д����ʱ��C�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
֤������ͼ1�У�����QP��
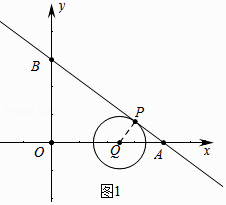
��Rt��AOB��OA=4��OB=3��
��AB= ![]() =5��
=5��
��AP=4t��AQ=5t��
�� ![]() =
= ![]() =
= ![]() ���ߡ�PAQ=��BAO��
���ߡ�PAQ=��BAO��
���PAQ�ס�BAO��
���APQ=��AOB=90�㣬
��QP��AB��
��AB�ǡ�O������
��2��
�⣺����ͼ2�У���ֱ��CM�ڡ�O��������Q����ʱ�����е�ΪD�����ı���PQDM�������Σ�
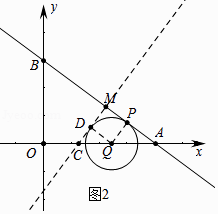
��֪PQ=DQ=3t��CQ= ![]() 3t=
3t= ![]() ��
��
��OC+CQ+AQ=4��
��m+ ![]() t+5t=4��
t+5t=4��
��m=4�� ![]() t��
t��
����ͼ3�У���ֱ��CM�ڡ�O���Ҳ����Q����ʱ�����е�ΪD�����ı���PQDM�������Σ�
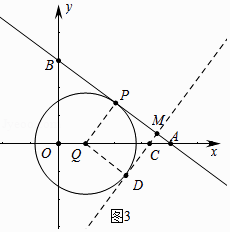
��OC+AQ��CQ=4��
��m+5t�� ![]() t=4��
t=4��
��m=4�� ![]() t
t
��3��
�⣺���ڣ��������£�
��ͼ4�У�����Q��y����Ҳ���y������ʱ��3t+5t=4��t= ![]() ��
��
�ɣ�2����֪��m=�� ![]() ��
�� ![]() ��
��
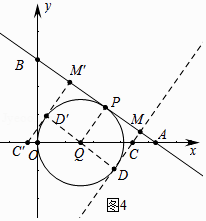
��ͼ5�У�����Q��y��������y������ʱ��5t��3t=4��t=2��
�ɣ�2����֪��m=�� ![]() ��
�� ![]() ��
��
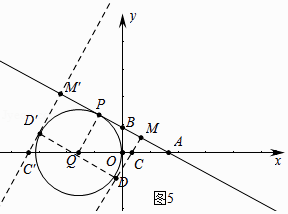
�������������������ĵ�C������Ϊ���� ![]() ��0����
��0���� ![]() ��0����
��0���� ![]() ��0����
��0���� ![]() ��0��
��0��
����������1��ֻҪ֤����PAQ�ס�BAO�������Ƴ���APQ=��OB=90�㣬�Ƴ�QP��AB���Ƴ�AB�ǡ�O�����ߣ���2��������������⼴�ɣ�����ͼ2�У���ֱ��CM�ڡ�O��������Q����ʱ�����е�ΪD�����ı���PQDM�������Σ�����ͼ3�У���ֱ��CM�ڡ�O���Ҳ����Q����ʱ�����е�ΪD�����ı���PQDM�������Σ��ֱ��г����̼��ɽ�����⣮��3���������������ۼ��ɣ�һ�����ĸ�������������
�����㾫�������ڱ��⿼���ֱ����Բ������λ�ù�ϵ�����ߵ����ʶ�������Ҫ�˽�ֱ����Բ������λ�ù�ϵ��������Ϊ���룻������������Ϊ�ཻ,����ֱ�߽���Բ�ĸ��ߣ�Բ��ֱ����Ψһ������Ϊ���У�����ֱ�߽���Բ�����ߣ����Ψһ�Ĺ���������е㣻���ߵ����ʣ�1�������е㴹ֱ�������뾶��ֱ����Բ������2�������е㴹ֱ�����ߵ�ֱ�߱ؾ���Բ��3��Բ�����ߴ�ֱ�ھ����е�İ뾶���ܵó���ȷ�𰸣�


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�������ABCD�У���֪AD��BC��AB=DC��AC��BD���ڵ�O���ӳ�BC��E��ʹ��CE=AD������DE�� 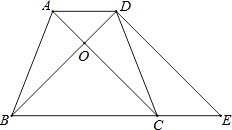
��1����֤��BD=DE��
��2����AC��BD��AD=3��SABCD=16����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��A��x��y��Ϊƽ��ֱ������ϵ�ڵĵ㣬������x=y����ѵ�A ������ƽ��㡱�����磺M��1��1����N����2��-2�����ǡ�ƽ��㡱������1��x��3 ʱ��ֱ��y=2x+m ���С�ƽ��㡱����m ��ȡֵ��Χ�ǣ� ��
A.0��m��1
B.��1��m��0
C.��3��m��3
D.��3��m��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2+��2k��1��x+k2��1=0������ʵ����x1 �� x2 ��
��1����ʵ��k��ȡֵ��Χ��
��2����x1 �� x2����x12+x22=16+x1x2 �� ��ʵ��k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У����ӶԽ���AC��BD������ABC��BC����ƽ�ƣ�ʹ��B�Ƶ���C���õ���DCE�� 
��1����֤����ACD�ա�EDC��
��2����̽����BDE����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ͬѧ��ÿ���㻨Ǯ�����УС������������˱�У����ͬѧ�����ݵ����������Ƴ������������в�������ͳ��ͼ���� ������ͳ�Ʊ�
��� | ���飨��λ��Ԫ�� | ���� |
A | 0��x��30 | 4 |
B | 30��x��60 | 16 |
C | 60��x��90 | a |
D | 90��x��120 | b |
E | x��120 | 2 |

���������ͼ��������������⣺
��1����գ���α������ͬѧ�����ˣ�a+b= �� m=��
��2��������ͳ��ͼ������C��Բ�ĽǶ�����
��3����У����ѧ��1000�ˣ������ÿ���㻨Ǯ������x��60��x��120��Χ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABCλ�ڵڶ����ޣ���A�������ǣ���2��3�����Ȱѡ�ABC����ƽ��4����λ���ȵõ���A1B1C1 �� �������A1B1C1����x��ԳƵġ�A2B2C2 �� ���A�Ķ�Ӧ��A2�������ǣ� ��
A.����3��2��
B.��2����3��
C.��1����2��
D.����1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ͳ��ͼ��ӳ���ҹ��롰һ��һ·�����߲��ֵ�����ó������� 2011��2016���ҹ��붫���ǵ����Ͷ�ŷ������ó��ͳ��ͼ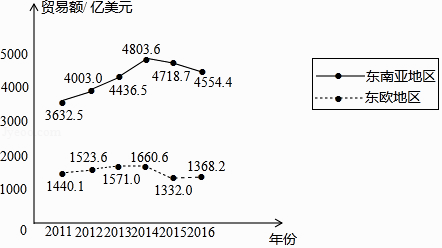
����������ժ�ԡ���һ��һ·��ó���������ݱ��棨2017������
����ͳ��ͼ�ṩ����Ϣ�������������������ǣ� ��
A.��2015����ȣ�2016���ҹ��붫ŷ������ó����������
B.2011��2016�꣬�ҹ��붫���ǵ�����ó����������
C.2011��2016�꣬�ҹ��붫���ǵ�����ó���ƽ��ֵ����4200����Ԫ
D.2016���ҹ��붫���ǵ�����ó����ҹ��붫ŷ������ó���3������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��BDΪԲO���������ഹֱ��ֱ��������P��Բ��O��������O��C��D��O��·���������˶������˶�ʱ��Ϊt�룬��APB�Ķ���Ϊy�ȣ���ô��ʾy��t֮�亯����ϵ��ͼ�����Ϊ�� ��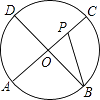
A.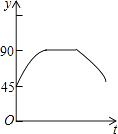
B.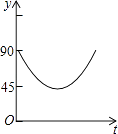
C.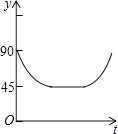
D.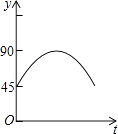
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com