
【题目】如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE. 
(1)求证:△ACD≌△EDC;
(2)请探究△BDE的形状,并说明理由.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=DC,AC=BD,AD=BC,∠ADC=∠ABC=90°,
由平移的性质得:DE=AC,CE=BC,∠DCE=∠ABC=90°,DC=AB,
∴AD=EC,
在△ACD和△EDC中, 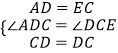 ,
,
∴△ACD≌△EDC(SAS)
(2)解:△BDE是等腰三角形;理由如下:
∵AC=BD,DE=AC,
∴BD=DE,
∴△BDE是等腰三角形
【解析】(1)由矩形的性质得出AB=DC,AC=BD,AD=BC,∠ADC=∠ABC=90°,由平移的性质得:DE=AC,CE=BC,∠DCE=∠ABC=90°,DC=AB,得出AD=EC,由SAS即可得出结论;(2)由AC=BD,DE=AC,得出BD=DE即可.
【考点精析】利用矩形的性质和平移的性质对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.


科目:初中数学 来源: 题型:
【题目】如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线y= ![]() x2+bx+c经过C、B两点,与x轴的另一交点为D.
x2+bx+c经过C、B两点,与x轴的另一交点为D.
(1)点B的坐标为( , ),抛物线的表达式为;
(2)如图2,求证:BD∥AC;
(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图. 
请根据统计图表提供的信息,解答下列问题:
(1)参加调查的人数共有人;在扇形图中,m=;将条形图补充完整;
(2)如果该校有3500名学生,则估计喜欢“篮球”的学生共有多少人?
(3)该社团计划从篮球、足球和乒乓球中,随机抽取两种球类组织比赛,请用树状图或列表法,求抽取到的两种球类恰好是“篮球”和“足球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如 ![]() ,表示a1=a2+a3 , 则a1的最小值为( )
,表示a1=a2+a3 , 则a1的最小值为( ) 
A.32
B.36
C.38
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中,∠BAO=90°,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
(1)如图1,若点B在OP上,则
①ACOE(填“<”,“=”或“>”);
②线段CA、CO、CD满足的等量关系式是;
(2)将图1中的等腰Rt△ABO绕O点顺时针旋转α(0°<α<45°),如图2,那么(1)中的结论②是否成立?请说明理由;
(3)将图1中的等腰Rt△ABO绕O点顺时针旋转α(45°<α<90°),请你在图3中画出图形,并直接写出线段CA、CO、CD满足的等量关系式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,直线y=﹣ ![]() x+3与x轴、y轴分别交于A、B两点,点P、Q同时从点A出发,运动时间为t秒.其中点P沿射线AB运动,速度为每秒4个单位长度,点Q沿射线AO运动,速度为每秒5个单位长度.以点Q为圆心,PQ长为半径作⊙Q.
x+3与x轴、y轴分别交于A、B两点,点P、Q同时从点A出发,运动时间为t秒.其中点P沿射线AB运动,速度为每秒4个单位长度,点Q沿射线AO运动,速度为每秒5个单位长度.以点Q为圆心,PQ长为半径作⊙Q.
(1)求证:直线AB是⊙Q的切线;
(2)过点A左侧x轴上的任意一点C(m,0),作直线AB的垂线CM,垂足为M.若CM与⊙Q相切于点D,求m与t的函数关系式(不需写出自变量的取值范围);
(3)在(2)的条件下,是否存在点C,直线AB、CM、y轴与⊙Q同时相切?若存在,请直接写出此时点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈ ![]() ,cos53°≈
,cos53°≈ ![]() ,tan53°≈
,tan53°≈ ![]() ,
, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性.
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点. 
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使锐角△AOB的面积等于3.求点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com