
【题目】在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:
已知:![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,将线段
,将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .当点
.当点![]() 在如图所示的位置时:
在如图所示的位置时:
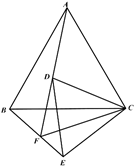
(1)观察填空:
①与![]() 全等的三角形是________;
全等的三角形是________;
②![]() 的度数为
的度数为
(2)利用题干中的结论,证明:![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆;
四点共圆;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.____________________.
之间的数量关系.____________________.
【答案】(1)①![]() :②
:②![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)①根据旋转的性质和等边三角形的性质可证△ACD≌△BCE;
②根据已推导出的全等三角形和三角形内角和进行角度转化,可得∠AFB的大小;
(2)根据△ACD≌△BCE得![]() ,推导得出四边形CDFE中
,推导得出四边形CDFE中![]() ,从而证共圆;
,从而证共圆;
(3)先推导出△BDF是等边三角形,可证△ABD≌△CBP,得出AD=FC,从而得出数量关系.
(1)①∵△ABC是等边三角形
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°
∵将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]()
∴CE=CD,∠DCE=60°
∴△DCE是等边三角形
∴∠DCE=60°
∵∠ACD+∠DCB=60°,∠BCE+∠DCB=60°
∴∠ACD=∠BCE
∴△ACD≌△BCE(SAS)
②∵△ACD≌△BCE
∴∠EBC=∠DAC
∵∠DAC+∠BAD=∠BAC=60°
∴∠FBC+∠BAD=60°
∴∠AFB=180°-∠ABC-∠FBC-∠BAF=180°-60°-60°=60°
(2)∵![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆;
四点共圆;
(证明不唯一)
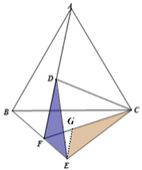
(3)结论:![]() ,如下图,连接BD
,如下图,连接BD
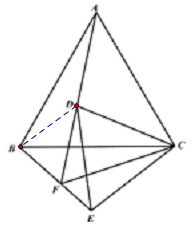
∵△ACD≌△BCE
∴∠CBE=∠CAD,AD=BE
∵∠CAD+∠BAD=60°,∠BAD+∠FBC=60°
∴∠BAD+∠ABD=∠BDF=60°
∵∠AFB=60°
∴△BDF是等边三角形
∴DF=BF,∴FD+FE=BE
∴△ABD≌△CBF(SAS)
∴AD=FC
∴FD+FE=FC


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是除0外的全体实数,
的取值范围是除0外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 1 | 2 | 3 | 6 | … |
| … | 1 | 2 |
| 6 | 1 | 3 | 2 | 1 | … |
其中,![]() _________.
_________.
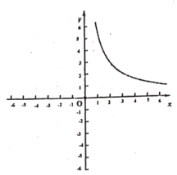
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出一条函数性质.
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________.
的实数根的情况是________.
②方程![]() 有_______个实效根;
有_______个实效根;
③关于![]() 的方程
的方程![]() 有2个实数根,
有2个实数根,![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.分析下列结论:①AP⊥BN;②BM=DN;③点P一定在以CM为直径的圆上;④正方形内不存在点P使得PC=![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
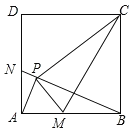
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
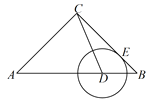
【题目】如图,△ABC中,AC=BC=4,∠ACB=90°,D为边AB上一动点(不与A、B重合),⊙D与BC切于E点,E点关于CD的对称点F在△ABC的一边上,则BD=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数
与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数![]() (
(![]() )的图像为直线
)的图像为直线![]() .
.
(1)求A、B两点的坐标;
(2)当1≤x≤2时,![]() ≤
≤![]() ≤
≤![]() ,试说明:抛物线G的顶点不在直线
,试说明:抛物线G的顶点不在直线![]() 上;
上;
(3)设![]() ,直线
,直线![]() 与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线
与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线![]() 距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
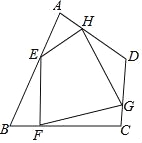
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,点E是AD边上的中点,BF平分∠EBC交CD于点F,过点F作FG⊥AB交BE于点H,则GH的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
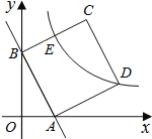
【题目】如图,直线AB:y=kx+b与x轴.y轴分别相交于点A(1,0)和点B(0,2),以线段AB为边在第一象限作正方形ABCD.
(1)求直线AB的解析式;
(2)求点D的坐标;
(3)若双曲线![]() (k>0)与正方形的边CD绐终有一个交点,求k的取值范围.
(k>0)与正方形的边CD绐终有一个交点,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com