
【题目】如图,直线AB:y=kx+b与x轴.y轴分别相交于点A(1,0)和点B(0,2),以线段AB为边在第一象限作正方形ABCD.
(1)求直线AB的解析式;
(2)求点D的坐标;
(3)若双曲线![]() (k>0)与正方形的边CD绐终有一个交点,求k的取值范围.
(k>0)与正方形的边CD绐终有一个交点,求k的取值范围.
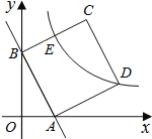
【答案】(1)y=-2x+2;(2)点D的坐标为(3,1);(3)3≤k≤6.
【解析】
(1)根据点A,B的坐标,利用待定系数法可求出直线AB的解析式;
(2)作DF⊥x轴于F,易证△ADF≌△BAO(AAS),利用全等三角形的性质可求出点D的坐标;
(3)同(2)可求出点C的坐标,利用极限值法可求出k的最大.最小值,此题得解.
解:(1)将A(1,0),B(0,2)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y=-2x+2.
(2)作DF⊥x轴于F,则∠AFD=90°,
∵正方形ABCD,
∴BA=AD,∠BAD=90°,∠BAO+∠DAF=90°,
∵∠BAO+∠ABO=90°,
∴∠ABO=∠DAF.
在△ADF和△BAO中,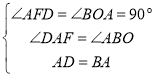 ,
,
∴△ADF≌△BAO(AAS),
∴AF=BO=2,DF=AO=1,OF=OA+AF=3,
∴点D的坐标为(3,1).

(3)同(2)可得出点C的坐标为(2,3).
当双曲线过点D时,k=3×1=3;
当双曲线过点C时,k=2×3=6,
∴当双曲线![]() (k>0)与正方形的边CD绐终有一个交点时,k的取值范围为3≤k≤6.
(k>0)与正方形的边CD绐终有一个交点时,k的取值范围为3≤k≤6.


科目:初中数学 来源: 题型:
【题目】在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:
已知:![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,将线段
,将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .当点
.当点![]() 在如图所示的位置时:
在如图所示的位置时:
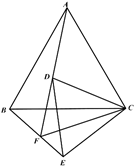
(1)观察填空:
①与![]() 全等的三角形是________;
全等的三角形是________;
②![]() 的度数为
的度数为
(2)利用题干中的结论,证明:![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆;
四点共圆;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.____________________.
之间的数量关系.____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
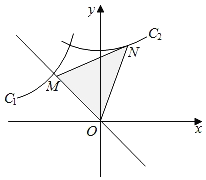
【题目】已知反比例函数C1:y=﹣![]() (x<0)的图象如图所示,将该曲线绕原点O顺时针旋转45°得到曲线C2,点N是曲线C2上的一点,点M在直线y=﹣x上,连接MN,ON,若MN=ON,则△MON的面积为_____.
(x<0)的图象如图所示,将该曲线绕原点O顺时针旋转45°得到曲线C2,点N是曲线C2上的一点,点M在直线y=﹣x上,连接MN,ON,若MN=ON,则△MON的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州包子是淮扬菜系的维扬点心代表,里面的馅品种丰富.早饭准备了四个包子,一个蟹黄包、一个松籽包、两个三鲜包,四个包子除馅外其他都相同.
(1)请预测“吃一个包子恰好是松籽包”的概率是_______;
(2)请用画树状图或用表格的方法预测“吃两个包子恰好是三鲜包”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
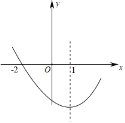
【题目】如图,二次函数![]() 的图象过点
的图象过点![]() ,对称轴为直线
,对称轴为直线![]() .有以下结论:
.有以下结论:
①![]() ;
;
②![]() ;
;
③若![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() )是抛物线上的两点,当
)是抛物线上的两点,当![]() 时,
时,![]() ;
;
④点![]() ,
,![]() 是抛物线与
是抛物线与![]() 轴的两个交点,若在
轴的两个交点,若在![]() 轴下方的抛物线上存在一点
轴下方的抛物线上存在一点![]() ,使得
,使得![]() ⊥
⊥![]() ,则
,则![]() 的取值范围为
的取值范围为![]() ;
;
⑤若方程![]() 的两根为
的两根为![]() ,
,![]() ,且
,且![]() <
<![]() ,则﹣2≤
,则﹣2≤![]() <
<![]() <4.
<4.
其中正确结论的序号是( )
A.①②④B.①③④
C.①③⑤D.①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数![]() ,以下结论:①抛物线交
,以下结论:①抛物线交![]() 轴有两个不同的交点;②不论
轴有两个不同的交点;②不论![]() 取何值,抛物线总是经过一个定点;③设抛物线交
取何值,抛物线总是经过一个定点;③设抛物线交![]() 轴于
轴于![]() 、
、![]() 两点,若
两点,若![]() ,则
,则![]() ;④抛物线的顶点在
;④抛物线的顶点在![]() 图象上;⑤抛物线交
图象上;⑤抛物线交![]() 轴于
轴于![]() 点,若
点,若![]() 是等腰三角形,则
是等腰三角形,则![]() ,
,![]() ,
,![]() .其中正确的序号是( )
.其中正确的序号是( )
A. ①②⑤ B. ②③④ C. ①④⑤ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
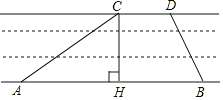
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量出AB=180m,CD=60m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04).

A.12.1mB.13.3m
C.16.9mD.18.1m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个![]() 奖品和2个
奖品和2个![]() 奖品共需120元;购买5个
奖品共需120元;购买5个![]() 奖品和4个
奖品和4个![]() 奖品共需210元.
奖品共需210元.
(1)求![]() ,
,![]() 两种奖品的单价;
两种奖品的单价;
(2)学校准备在获奖的2名男生3名女生中选两名同学参加县上的比赛,请问选中两名选手都是女孩的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com