
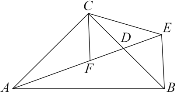
【题目】如图,在△ABC中,∠ACB = 90°,AC = BC,D为BC边的中点,BE⊥AB交AD的延长线于点E,CF平分∠ACB交AD于点F,连接CE.求证:(1)点D是EF的中点;(2)△CEF是等腰三角形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据题意已知条件证明△CDF≌△BDE即可求解;
(2)先证明△ACF≌△CBE 得到∠CAF=∠BCE ,从而得到∠ECF=∠CFE,即可求解.
(1)∵∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵BE⊥AB
∴∠ABE=90°
∴∠DBE=90°-45°=45°
∵CF 平分∠ACB
∴∠FCD=∠FCA=90°×![]() °
°
∴∠DBE=∠FCD
又∵D 为 BC 边的中点,
∴CD=BD
在△ CDF 与△BDE 中,
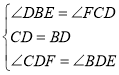
∴△CDF≌△BDE(ASA)
∴DF=DE
即点D是EF 的中点.
(2)∵∠ACF=45°,∠CBE=45°
∴∠ACF=∠CBE
又∵AC=BC,CF=BE
∴△ ACF≌△CBE(SAS)
∴∠CAF=∠BCE
∵∠ECF=45°+∠BCE ,∠CFE=∠ACF+∠CAF=45°+∠CAF
∴∠ECF=∠CFE
∴CE=FE
即△CEF是等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点H为BD中点,CH的延长线交AB于点F.
(1)求证:CH=EH;
(2)若∠CAB=40°,求∠EHF;
(3)如图②,若△DAE≌△CEH,点Q为CH的中点,连接AQ,求证:AQ∥EH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙为两座建筑物,它们之间的水平距离BC为30日,在A点测得D点的仰角∠EAD=45°,在B点测得D点的仰角为∠CBD=60°,测得甲、乙这两座建筑物的高度分别为( )米.

A. 10![]() ,30 B. 30,30
,30 B. 30,30![]() C. 30
C. 30![]() ﹣3,30 D. 30
﹣3,30 D. 30![]() ﹣30,30
﹣30,30![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,∠A=60°,CD、CE分别是△ABC的高和中线,下列说法错误的是( )
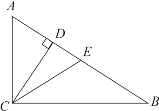
A.AD =![]() ABB.S△CEB = S△ACE
ABB.S△CEB = S△ACE
C.AC、BC的垂直平分线都经过ED.图中只有一个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是反比例函数
是反比例函数![]() 在第一象限图象上一点,点
在第一象限图象上一点,点![]() 的坐标为
的坐标为![]() .
.

![]() 当点
当点![]() 的横坐标逐渐增大时,
的横坐标逐渐增大时,![]() 的面积将如何变化?
的面积将如何变化?
![]() 若
若![]() 与
与![]() 均为直角三角形,其中
均为直角三角形,其中![]() ,求此反比例函数的解析式及点
,求此反比例函数的解析式及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
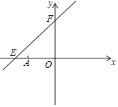
【题目】如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0),点P是直线EF上的一个动点.
(1)求k的值;
(2)点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;
(3)探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗,若能,请求出点P的坐标;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
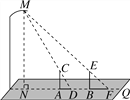
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com