
【题目】如图①,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点H为BD中点,CH的延长线交AB于点F.
(1)求证:CH=EH;
(2)若∠CAB=40°,求∠EHF;
(3)如图②,若△DAE≌△CEH,点Q为CH的中点,连接AQ,求证:AQ∥EH.
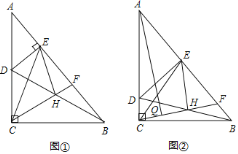
【答案】(1)见解析;(2)∠EHF=80°;(3)见解析
【解析】
(1)根据直角三角形斜边中线的性质证明即可.
(2)先根据等腰三角形的性质得:∠HCB=∠HBC,∠HEB=∠HBE,由三角形外角的性质得:∠DHC=2∠HBC,∠DHE=2∠HBE,从而有∠CHE=2∠CBA,计算∠CBA=50°,根据平角的定义可得结论;
(3)如图②,连接AH,先证明AE=ED=EH=DH=CH,得△DEH是等边三角形,所以∠DHC=30°,∠AEH=150°,再证明AC=AH,根据等腰三角形三线合一可得AQ⊥CH,最后根据同位角相等,两直线平行可得结论.
(1)证明:如图①,∵DE⊥AB,
∴∠DEB=90°,
在Rt△DEB和Rt△DCB中,∠DEB=∠DCB=90°,H为BD的中点,
∴EH=![]() BD,CH=
BD,CH=![]() BD,
BD,
∴EH=CH;
(2)解:∵H为BD的中点,
∴BH=![]() BD,
BD,
∴BH=EH=CH,
∴∠HCB=∠HBC,∠HEB=∠HBE,
在△CHB和△EHB中,
∠DHC=∠HCB+∠HBC,∠DHE=∠HEB+∠HBE,
∴∠DHC=2∠HBC,∠DHE=2∠HBE,
∴∠CHE=2∠CBA,
在Rt△ACB中,∠ACB=90°,
∴∠A+∠CBA=90°,
∵∠A=40°,
∴∠CBA=50°,
∴∠CHE=100°,
∴∠EHF=80°;
(3)证明:如图②,连接AH,
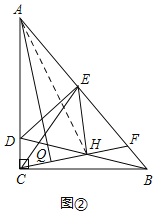
∵△DAE≌△CEH,
∴AE=EH,∠AED=∠EHC=90°,
∵HC=HE,DH=![]() BD,
BD,
∴AE=ED=EH=DH=CH,
∴△DEH是等边三角形,
∴∠DEH=∠DHE=60°,
∴∠DHC=∠EHC﹣∠EHD=30°,∠AEH=∠AED+∠DEH=150°,
∵AE=EH,DH=CH,
∴∠EHA=(180°﹣∠AEH)÷2=15°,
∠HCD=(180°﹣∠DHC)÷2=75°,
∴∠AHC=∠EHC﹣∠EHA=75°,
∴∠AHC=∠ACH=75°,
∴AC=AH,
∵Q是CH的中点,
∴AQ⊥CH,
∴∠AQC=90°,
∴∠AQC=∠EHC,
∴AQ∥EH.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】兰州市外国语学校开展“数学史”知识竞赛活动,八年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
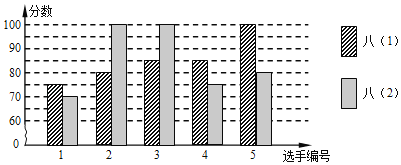
(1)请计算八(1)班、八(2)班选出的5名选手复赛的平均成绩?众数和中位数?
(2)请用方差判断哪个班选出的5名选手的复赛成绩比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点坐标
图象的一部分,抛物线的顶点坐标![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,下列结论:
两点,下列结论:
①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个相等的实数根;④抛物线与
有两个相等的实数根;④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;⑤当
;⑤当![]() 时,有
时,有![]() ,
,
其中正确的是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC和△DEF相似,则关于位似中心与相似比叙述正确的是( )

A. 位似中心是点B,相似比是2:1 B. 位似中心是点D,相似比是2:1
C. 位似中心在点G,H之间,相似比为2:1 D. 位似中心在点G,H之间,相似比为1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由边长相等的小正方形组成的网格,以下各图中点A、B、C、D都在格点上.
(1)在图1中,PC:PB= ;
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图2,在AB上找点P,使得AP:PB=1:3;
②如图3,在BC上找点P,使得△APB∽△DPC;
③如图4,在△ABC中内找一点P,连接PA、PB、PC,将△ABC分成面积相等的三部分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形A'B'C'D'在矩形ABCD的内部,AB∥A'B',AD∥A'D',且AD=12,AB=6,设AB与A'B'、BC与B'C'、CD与C'D'、DA与D'A'之间的距离分别为a,b,c,d,
(1)a=b=c=d=2,矩形A'B'C'D'∽矩形ABCD吗,为什么?
(2)若矩形A'B'C'D'∽矩形ABCD,a,b,c,d应满足什么等量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB = 90°,AC = BC,D为BC边的中点,BE⊥AB交AD的延长线于点E,CF平分∠ACB交AD于点F,连接CE.求证:(1)点D是EF的中点;(2)△CEF是等腰三角形.
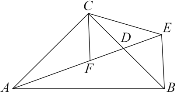
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com