
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点坐标
图象的一部分,抛物线的顶点坐标![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,下列结论:
两点,下列结论:
①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个相等的实数根;④抛物线与
有两个相等的实数根;④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;⑤当
;⑤当![]() 时,有
时,有![]() ,
,
其中正确的是________.

【答案】①③⑤
【解析】
利用对称轴是直线x=1判定①;利用开口方向,对称轴与y轴的交点判定a、b、c得出②;利用顶点坐标和平移的规律判定③;利用对称轴和二次函数的对称性判定④;利用图象直接判定⑤即可.
∵对称轴x= ![]() =1,
=1,
∴2a+b=0,①正确;
∵a<0,
∴b>0,
∵抛物线与y轴的交点在正半轴上,
∴c>0,
∴abc<0,②错误;
令y=3,得到ax2+bx+c=3,对应的点就是顶点,只有一个.
∴方程ax2+bx+c=3有两个相等的实数根,③正确;
∵对称轴是直线x=1,与x轴的一个交点是(4,0),
∴与x轴的另一个交点是(2,0),④错误;
∵当1<x<4时,由图象可知y2<y1,
∴⑤正确.
正确的有①③⑤.
故答案为:①③⑤.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】某工程队在我市实施棚户区改造过程中承包了一项拆迁工程.原计划每天拆迁![]() ,因为准备工作不足,第一天少拆迁了
,因为准备工作不足,第一天少拆迁了![]() .从第二天开始,该工程队加快了拆迁速度,第三天拆迁了
.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了![]() .求:
.求:
![]() 该工程队第一天拆迁的面积;
该工程队第一天拆迁的面积;
![]() 若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.
若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2 -(m+1)x+2(m-1)=0,
(1)求证:无论m取何值时,方程总有实数根;
(2)若等腰三角形腰长为4,另两边恰好是此方程的根,求此三角形的另外两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图l、图2和图3所示(阴影部分为草坪).

请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图l,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为考察两名实习工人的工作情况,质检部将他们工作某一周每天生产合格产品的个数整理成甲、乙两组数据,如下表:
甲 | 2 | 6 | 7 | 7 | 8 |
乙 | 2 | 4 | 5 | 8 | 8 |
根据以上数据,下面说法正确的是( )
A.甲、乙的众数相同B.甲、乙的中位数相同
C.甲的平均数小于乙的平均数D.甲的方差小于乙的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知二次函数的图象经过点
,已知二次函数的图象经过点![]() 、
、![]() 和点
和点![]() .
.

![]() 求
求![]() 、
、![]() 两点坐标;
两点坐标;
![]() 求该二次函数的关系式
求该二次函数的关系式
![]() 若抛物线的对称轴与
若抛物线的对称轴与![]() 轴的交点为点
轴的交点为点![]() ,则在抛物线的对称轴上是否存在点
,则在抛物线的对称轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形?如果存在,直接写出
为腰的等腰三角形?如果存在,直接写出![]() 点的坐标;如果不存在,请说明理由;
点的坐标;如果不存在,请说明理由;
![]() 点
点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线与抛物线相交于点
轴的垂线与抛物线相交于点![]() ,当点
,当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出四边形
的面积最大?求出四边形![]() 的最大面积及此时
的最大面积及此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
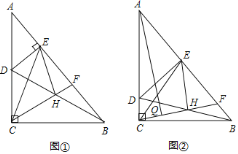
【题目】如图①,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点H为BD中点,CH的延长线交AB于点F.
(1)求证:CH=EH;
(2)若∠CAB=40°,求∠EHF;
(3)如图②,若△DAE≌△CEH,点Q为CH的中点,连接AQ,求证:AQ∥EH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com