
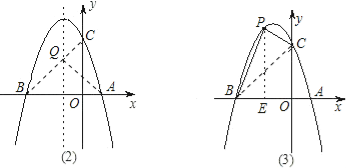
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
【答案】(1)抛物线解析式为:y=-x2-2x+3;
(2)存在,Q(-1,2);
(3)存在,点P坐标为(-![]() ,
,![]() ),S△BPC最大=
),S△BPC最大=![]() ;
;
【解析】试题分析:(1)、将点A和点B代入函数解析式,利用待定系数法求出函数解析式;(2)、根据题意得出A、B两点关于对称轴对称,则直线BC与x=-1的交点就是点Q,根据题意得出点C的坐标,然后利用待定系数法求出直线BC的解析式,从而得出点Q的坐标;(3)、首先设点P的坐标,然后根据△BPC的面积等于四边形BPCO的面积减去△BOC的面积,然后列出关于x的函数解析式,从而得出最大值.
试题解析:(1)、将A(1,0),B(﹣3,0)代y=﹣x2+bx+c中得
![]() ∴
∴![]() ∴抛物线解析式为:y=﹣x2﹣2x+3;
∴抛物线解析式为:y=﹣x2﹣2x+3;
(2)、存在
理由如下:由题知A、B两点关于抛物线的对称轴x=﹣1对称
∴直线BC与x=﹣1的交点即为Q点,此时△AQC周长最小∵y=﹣x2﹣2x+3 ∴C的坐标为:(0,3)
直线BC解析式为:y="x+3" Q点坐标即为![]() 解得
解得![]() ∴Q(﹣1,2);
∴Q(﹣1,2);
(3)、存在.
理由如下:设P点(x,﹣x2﹣2x+3)(﹣3<x<0) ∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣![]()
若S四边形BPCO有最大值,则S△BPC就最大,
∴S四边形BPCO=S△BPE+S直角梯形PEOC=![]() BEPE+
BEPE+![]() OE(PE+OC)=
OE(PE+OC)=![]() (x+3)(﹣x2﹣2x+3)+
(x+3)(﹣x2﹣2x+3)+![]() (﹣x)(﹣x2﹣2x+3+3)
(﹣x)(﹣x2﹣2x+3+3)
=![]()
当x=﹣![]() 时,S四边形BPCO最大值=
时,S四边形BPCO最大值=![]() ∴S△BPC最大=
∴S△BPC最大=![]()
当x=﹣![]() 时,﹣x2﹣2x+3=
时,﹣x2﹣2x+3=![]() ∴点P坐标为(﹣
∴点P坐标为(﹣![]() ,
,![]() ).
).


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】在元旦期间,某商场投入13800元资金购进甲、乙两种商品共500件,两种商品的成本价和销售价如下表所示:
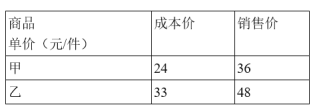
(1)该商场购进两种商品各多少件?
(2)这批商品全部销售完后,该商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍海洋资源,保护海洋生物多科性“的知识党春活动,为了解此次宛赛成镇(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图(如图):

请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了_____个参赛学生的成绩;
(2)a=_____,b=_____.
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是_____
(4)请你估计,该校八年级全年级有500名学生,竞赛成绩达到80分以上(含80分)的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点坐标
图象的一部分,抛物线的顶点坐标![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,下列结论:
两点,下列结论:
①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个相等的实数根;④抛物线与
有两个相等的实数根;④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;⑤当
;⑤当![]() 时,有
时,有![]() ,
,
其中正确的是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 填空:
填空:![]() ________;
________;
![]() 点
点![]() 在抛物线上,且
在抛物线上,且![]() ,求
,求![]() 面积的最大值;
面积的最大值;
![]() 设
设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒一个单位速度运动到
以每秒一个单位速度运动到![]() 点,再沿线段
点,再沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止,当点
后停止,当点![]() 的坐标是多少时,点
的坐标是多少时,点![]() 在整个运动中用时最少?
在整个运动中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标平面内的两点A(3,2),点B (6,0)过点B作Y轴的平行线交直线OA于点C
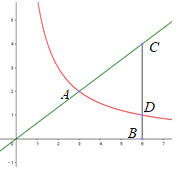
(1)求直线OA所对应的函数解析式
(2)若某一个反比例函数的图像经过点A,且交BC于点D,联结AD,求△ACD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com