
【题目】已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE

(1)如图1,当AE平分∠BAC时,EH⊥AB于H,△EHB的周长为10m,求AB的长;
(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.
【答案】(1)AB=10m;(2)见解析.
【解析】
(1)根据等腰三角形的性质得到∠B=45°,根据角平分线的性质得到CE=EH=BH,根据全等三角形的性质得到AH=AC,于是得到结论;
(2)先连接AD,依据AAS判定△ADF≌△ABE,得到DF=BE,再判定△BCG≌△DCF,得出DF=BG,进而得到BG=BE.
解:(1)∵∠ACB=90°,AC=BC,
∴∠B=45°,
∵AE平分∠BAC时,EH⊥AB于H,
∴CE=EH=BH,
在Rt△ACE与Rt△AHE中,
![]() ,
,
∴Rt△ACE与Rt△AHE(HL),
∴AH=AC,
∴AH=BC,
∵△EHB的周长为10m,
∴AB=AH+BH=BC+BH=10m;
(2)如图所示,连接AD,
线段AE绕点A顺时针旋转90°得线段AF,则AE=AF,∠EAF=90°,
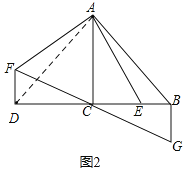
∵AC⊥BD,DC=BC,
∴AD=AB,∠ABE=∠ADC=45°,
∴∠BAD=90°=∠EAF,
∴∠BAE=∠DAF,
∴△ABE≌△ADF(SAS),
∴DF=BE,∠ADF=∠ABE=45°,
∴∠FDC=90°,
∵BG⊥BC,
∴∠CBG=∠CDF=90°,
又∵BC=DC,∠BCG=∠DCF,
∴△BCG≌△DCF(ASA),
∴DF=BG,
∴BG=BE.


科目:初中数学 来源: 题型:
【题目】如图,![]() 在
在![]() 的正北方向,
的正北方向,![]() 在
在![]() 的正东方向,且
的正东方向,且![]() .某一时刻,甲车从
.某一时刻,甲车从![]() 出发,以
出发,以![]() 的速度朝正东方向行驶,与此同时,乙车从
的速度朝正东方向行驶,与此同时,乙车从![]() 出发,以
出发,以![]() 的速度朝正北方向行驶.
的速度朝正北方向行驶.![]() 小时后,位于点
小时后,位于点![]() 处的观察员发现甲、乙两车之间的夹角为
处的观察员发现甲、乙两车之间的夹角为![]() ,即
,即![]() ,此时,甲、乙两人相距的距离为( )
,此时,甲、乙两人相距的距离为( )

A. 90km B. 50![]() km C. 20
km C. 20![]() km D. 100km
km D. 100km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,点 D,E 分别在∠ABC 和∠ACB 的平分线上,连接 BD,DE,EC,若∠D+∠E=295°, 则∠A 是( )
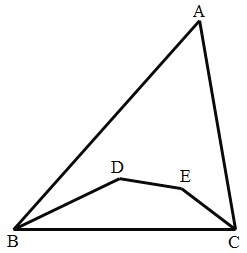
A.65°B.60°C.55°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
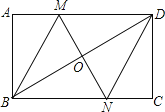
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
![]() 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形;
![]() 若
若![]() ,
,![]() ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )

A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
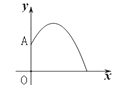
【题目】某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是![]() ,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有( )
,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com