
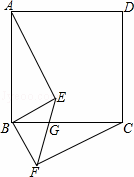
如图,四边形ABCD是正方 形,BE⊥BF,BE=BF,EF与BC交于点G.
形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
科目:初中数学 来源: 题型:
荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )
A. 1cm<AB<4cm B.5cm<AB<10cm C.4cm<AB<8cm D. 4cm<AB<10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
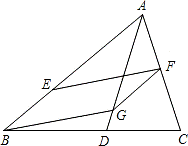
如图,在△ABC中,AD平分∠BAC交BC于点D.点E、F分别在边AB、AC上,且BE=AF,FG∥AB交线段AD于点G,连接BG、EF.
(1)求证:四边形BGFE是平行四边形;
(2)若△ABG∽△AGF,AB=10,AG=6,求线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com