Question

【题目】△ABC是等边三角形，点C关于AB对称的点为C′，点P是直线C′B上的一个动点，连接AP，作∠APD＝60°交射线BC于点D．

（1）若点P在线段C′B上（不与点C′，点B重合）

①如图1，当点P是线段C′B的中点时，直接写出线段PD与线段PA的数量关系　 　．

②如图2，点P是线段C′B上任意一点，证明PD与PA的数量关系．

（2）若点P在线段C′B的延长线上，

①依题意补全图3；

②直接写出线段BD，AB，BP之间的数量关系为：　 　．

Answer 1

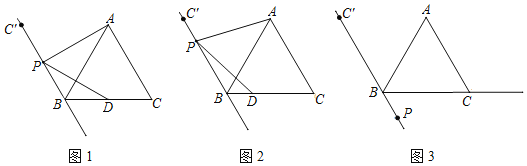
【答案】（1）①PD＝PA；②详见解析；（2）①详见解析；②BD＝BP+AB．

【解析】

（1）①如图1中，连接AC′，可证△ABC′是等边三角形，由PB＝PC′，推出PA⊥BC′，可求∠BDP＝∠BPD＝30°，可得PB＝PD，由“SAS”可证△ABD≌△ABP，可得AP＝AD，由等边三角形的性质可求解；

②如图2中，作∠BPE＝60°交AB于点E，只要证明△PBD≌△PEA（ASA）即可解决问题；

（2）①根据要求画出图形即可解决问题；

②结论：BD＝BP+AB．如图3中，在BD上取一点E，使得BE＝PB．只要证明△BPA≌△EPD（SAS），即可解决问题．

（1）①解：如图1中，连接AC′．

∵△ABC是等边三角形，

∴∠ABC＝60°，

∵点C'与点C关于AB对称，

∴∠C'BA＝∠CBA＝60°，BC′＝BC＝BA，

∴△ABC′是等边三角形，

∵PB＝PC′，

∴PA⊥BC′，且∠APD＝60°，

∴∠BPD＝30°，且∠PBD＝120°

∴∠BDP＝∠BPD＝30°，

∴PB＝BD，且∠ABC＝∠ABC'＝60°，AB＝AB，

∴△ABD≌△ABP（SAS）

∴AP＝AD，且∠APD＝60°，

∴△APD是等边三角形，

∴AP＝PD，

故答案为AP＝PD．

②证明：如图2中，作∠BPE＝60°交AB于点E．

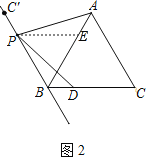
∵△ABC是等边三角形，

∴∠ABC＝60°，

∵点C'与点C关于AB对称，

∴∠C'BA＝∠CBA＝60°＝∠BPE，

∴∠PEB＝60°．

∴△PBE是等边三角形，

∴PB＝PE，AEP＝120°＝∠PBD．

∵∠BPD+∠DPE＝60°，∠APE+∠DPE＝60°，

∴∠BPD＝∠APE，

在△PBD和△PEA中，

∴△PBD≌△PEA（ASA）．

∴PD＝PA．

（2）①解：补全图形，如图3所示：

②解：结论：BD＝BP+AB．

理由：如图3中，在BD上取一点E，使得BE＝PB．

∵∠EBP＝60°，BE＝BP，

∴△EBP是等边三角形，

由（1）可知：△PAD是等边三角形，

∴∠BPE＝∠APD＝60°，

∴∠APB＝∠EPD，

∵PB＝PE，PA＝PD，

∴△BPA≌△EPD（SAS），

∴AB＝DE，

∴BD＝BE+ED＝BP+AB．

故答案为BD＝BP+AB．