
分析 对一个多项式进行因式分解时,当要求在实数范围内进行因式分解时,分解的式子的结果一般要分到出现无理数为止.本题4m4和16分别是2m2和22的平方,并且符号相反,因此可采用平方差公式进行分解,分解后再根据式子特点继续分解.
解答 解:4m4-16
=4m4-24
=(2m2+22)(2m2-22)
=4(m2+2)(m+$\sqrt{2}$)(m-$\sqrt{2}$).
故答案为:4(m2+2)(m+$\sqrt{2}$)(m-$\sqrt{2}$).
点评 本题考查实数范围内的因式分解,因式分解的步骤为:一提公因式;二看公式.在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止.


科目:初中数学 来源: 题型:解答题
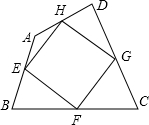 如图,四边形ABCD中,E,F,G,H分别是AB、BC、CD、DA的中点.
如图,四边形ABCD中,E,F,G,H分别是AB、BC、CD、DA的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
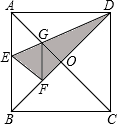 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小明按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小明按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
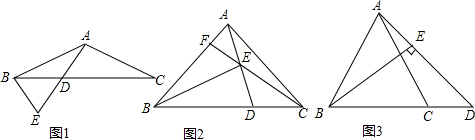
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
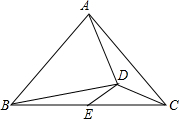 如图,在△ABC中,AB=AC,∠BAC=90°,点D在△ABC内部,AB=BD,AD=$\sqrt{2}$CD,E为BC边的中点,连接DE,若S△ACD=1,则线段DE的长为1.
如图,在△ABC中,AB=AC,∠BAC=90°,点D在△ABC内部,AB=BD,AD=$\sqrt{2}$CD,E为BC边的中点,连接DE,若S△ACD=1,则线段DE的长为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com