【题目】如图，已知A、B两点的坐标分别为（2，0）、（0，2），⊙C的圆心坐标为(﹣1，0)，半径为1．若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是（ ）
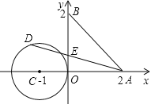
A. 2 B. 1 C. 
D. 
学而优衔接教材南京大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，D为⊙O上一点，过弧BD上一点T作⊙O的切线TC，且TC⊥AD于点C．
（1）若∠DAB＝50°，求∠ATC的度数；
（2）若⊙O半径为2，TC＝
，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有四张正面分别标有数字﹣1，0，1，2的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上洗均匀．
（1）随机抽取一张卡片，求抽到数字“﹣1”的概率；
（2）随机抽取一张卡片，然后不放回，再随机抽取一张卡片，请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：点P（m，4）在反比例函数y＝﹣
的图象上，正比例函数的图象经过点P和点Q（6，n）．
（1）求正比例函数的解析式；
（2）求P、Q两点之间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明和小亮利用三张卡片做游戏，卡片上分别写有A，B，B．这些卡片除字母外完全相同，从中随机摸出一张，记下字母后放回，充分洗匀后，再从中摸出一张，如果两次摸到卡片字母相同则小明胜，否则小亮胜，这个游戏对双方公平吗？请说明现由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，四边形OABC是矩形，点A的坐标为（3，0），点C的坐标为（0，6），点P从点O出发，沿OA以每秒1个单位长度的速度向点A出发，同时点Q从点A出发，沿AB以每秒2个单位长度的速度向点B运动，当点P与点A重合时运动停止．设运动时间为t秒．
（1）当t=2时，线段PQ的中点坐标为_____；
（2）当△CBQ与△PAQ相似时，求t的值；
（3）当t=1时，抛物线y=x2+bx+c经过P，Q两点，与y轴交于点M，抛物线的顶点为K，如图2所示，问该抛物线上是否存在点D，使∠MQD=
∠MKQ？若存在，求出所有满足条件的D的坐标；若不存在，说明理由．
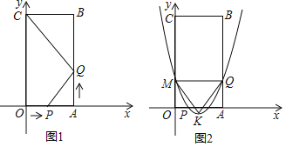
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在“国学经典”主题比赛活动中，甲、乙、丙三位同学的三项比赛成绩如下表（单位：分）．
国学知识 | 现场写作 | 经典诵读 | |
甲 | 86 | 70 | 90 |
乙 | 86 | 80 | 90 |
丙 | 86 | 85 | 90 |
（1）若“国学知识”、“现场写作”“经典诵读”分别按30%，20%，50%的比例计入该同学的比赛得分，请分别计算甲、乙两位同学的得分；
（2）若甲同学的得分是80分，乙同学的得分是84分，则丙同学的得分是______分．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明同学用纸板制作了一个圆锥形漏斗模型．如图所示，它的底面半径OB＝3cm，高OC＝4cm，这个圆锥漏斗的侧面积是多少？侧面展开图所对的圆心角是多少度？
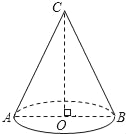
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某山区学校为开发学生特长，培养兴趣爱好，准备开设“第二课堂培训班”，每周进行一次．拟开设科目有：A．数学兴趣，B．古诗词欣赏；C．英语特长；D．艺术赏析；E．竞技体育等五类．学校对学生进行了抽样调查（每人只能选择一项），并将调查结果绘制成图1和图2所示的两个不完整统计图．
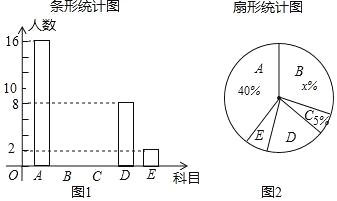
根据以上信息，解答下列问题：
（1）求x的值，并将图1补充完整；
（2）在图2中，D科目所占扇形圆心角的度数为_____；
（3）为提高学生对C、E科目的了解与关注，学校准备从选C、E科目的学生中随机选出2名出黑板报进行宣传，请你用列表法或树状图法求这2名同学选择不同科目的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
