
���� [������֤��]������ƽ���ı��ε����ʵó���GAC=��ACB���ɷ��۵����ʵó���ACB=��ACB�䣬֤����GAC=��ACB�䣬�ó�AG=CG��
�ڵó�DG=B��G��֤����CB��D=��B��DA=$\frac{1}{2}$��180��-��B��GD�����ɡ�AGC=��B��GD���ó���ACB��=��CB��D�����ɵó�B��D��AC��
��Ӧ�����𡿣���CF��AB����F��ͨ����ֱ�����������CF=$\frac{1}{2}$��B��F=$\frac{\sqrt{3}}{2}$���������AF=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$����AE=CE=x����EF=$\frac{3\sqrt{3}}{2}$-x�����ݹ��ɶ����������xֵ����AE��ֵ��Ȼ����������ε������ʽ������á�AEC�������
����չ��̽��������֤���ı���ACB��D�ǵ������Σ����ݵ������ε����ʵó���AB��C=��CDA=30�㣬��B��AD=��DCB��=90�㣬���ADB��=��CB��D=y�����AB��D=y-30�㣬���ݡ�AB��D+��ADB��=90�㣬�ó�y-30��+y=90�㣬���y=60�㣬������á�AB��D=30�㣬ͨ����ֱ�������μ������BC��
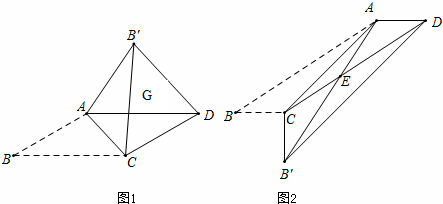
��� �⣺��������֤��������ͼ1��
�١��ı���ABCD��ƽ���ı��Σ�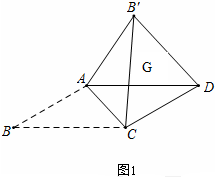
��AD��BC��
���DAC=��ACB��
�߽���ABC��AC��������AB��C��
���ACB��=��ACB��
���DAC=��ACB�䣬
��AG=CG��
���AGC�ǵ��������Σ�
�ڡ��ı���ABCD��ƽ���ı��Σ�
��AD=BC��
�߽���ABC��AC��������AB��C��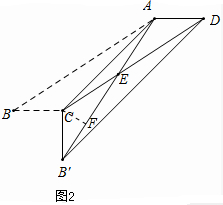
��B��C=BC��
��B��C=AD��
��B��G=DG��
���CB��D=��ADB�䣬
�ߡ�AGC=��B��GD����ACB��=��CAD��
���ADB��=��DAC��
��B��D��AC��
��Ӧ�����𡿣���ͼ2��
��CF��AB����F��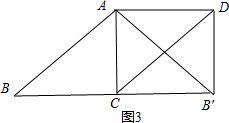
�ߡ�B=30�㣬
���AB��C=30�㣬
��CF=$\frac{1}{2}$B��C=$\frac{1}{2}$BC=$\frac{1}{2}$��B��F=$\frac{\sqrt{3}}{2}$B��C=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$��
��AB��=AB=2$\sqrt{3}$��
��AF=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$��
��AE=CE=x����EF=$\frac{3\sqrt{3}}{2}$-x��
��CF2+EF2=CE2��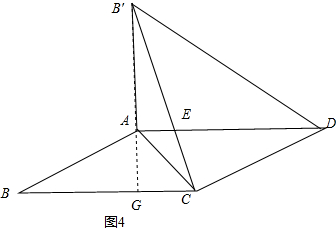
�ࣨ$\frac{1}{2}$��2+��$\frac{3\sqrt{3}}{2}$-x��2=x2��
���x=$\frac{7\sqrt{3}}{9}$��
��AE=$\frac{7\sqrt{3}}{9}$��
���AEC�����=$\frac{1}{2}$AE•CF=$\frac{1}{2}$��$\frac{7\sqrt{3}}{9}$��$\frac{1}{2}$=$\frac{7\sqrt{3}}{36}$��
����չ��̽��������ͼ2��
��AD=BC��BC=B��C��
��AD=B��C��
��AC��B��D��
���ı���ACB��D�ǵ������Σ�
�ߡ�B=30�㣬���AB��C=��CDA=30�㣬
�ߡ�AB��D��ֱ�������Σ�
����B��AD=90�㣬AB��BCʱ��
���ADB��=��CB��D=y��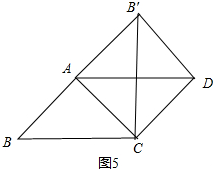
���AB��D=y-30�㣬
�ߡ�AB��D+��ADB��=90�㣬
��y-30��+y=90�㣬
���y=60�㣬
���AB��D=y-30��=30�㣬
��AB��=AB=2$\sqrt{3}$��
��AD=$\frac{\sqrt{3}}{3}$��2$\sqrt{3}$=2��
��BC=2��
����ADB��=90�㣬AB��BCʱ����ͼ3��
��AD=BC��BC=B��C��
��AD=B��C��
��AC��B��D��
���ı���ACB��D�ǵ������Σ�
�ߡ�ADB��=90�㣬
���ı���ACB��D�Ǿ��Σ�
���ACB��=90�㣬
���ACB=90�㣬
�ߡ�B=30�㣬AB=2$\sqrt{3}$��
��BC=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$��2$\sqrt{3}$=3��
����B��AD=90��AB��BCʱ����ͼ4��
��AD=BC��BC=B��C��
��AD=B��C��
��AC��B��D����B��AD=90�㣬
���B��GC=90�㣬
�ߡ�B=30�㣬AB=2$\sqrt{3}$��
���AB��C=30�㣬
��GC=$\frac{1}{2}$B��C=$\frac{1}{2}$BC��
��G��BC���е㣬
��RT��ABG��BG=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$��2$\sqrt{3}$=3��
��BC=6��
����AB��D=90��ʱ����ͼ5��
��AD=BC��BC=B��C��
��AD=B��C��
��AC��B��D��
���ı���ACDB���ǵ������Σ�
�ߡ�AB��D=90�㣬
���ı���ACDB���Ǿ��Σ�
���BAC=90�㣬
�ߡ�B=30�㣬AB=2$\sqrt{3}$��
��BC=AB��$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$��$\frac{1}{\frac{\sqrt{3}}{2}}$=4��
����֪��BC�ij�Ϊ2��3��4��6ʱ����AB��D��ֱ�������Σ�
���� ������Ҫ�����˷��۱任�����ʼ���Ӧ�����⣬��������йض������������жϡ��������𣬡���չ��̽�������ܹ��������ۣ�ȷ�������������ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
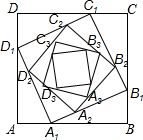 ��ͼ��������ABCD�ı߳�Ϊa����AB��BC��CD��DA���Ϸֱ�ȡ��A1��B1��C1��D1��ʹAA1=BB1=CC1=DD1=$\frac{1}{3}$a���ڱ�A1B1��B1C1��C1D1��D1A1�Ϸֱ�ȡ��A2��B2��C2��D2��ʹA1A2=B1B2=C1C2=D1D2=$\frac{1}{3}$A1B2���������ι��ɼ�����ȥ����������AnBnCnDn�����Ϊ$\frac{{5}^{n}}{{9}^{n}}{a}^{2}$��
��ͼ��������ABCD�ı߳�Ϊa����AB��BC��CD��DA���Ϸֱ�ȡ��A1��B1��C1��D1��ʹAA1=BB1=CC1=DD1=$\frac{1}{3}$a���ڱ�A1B1��B1C1��C1D1��D1A1�Ϸֱ�ȡ��A2��B2��C2��D2��ʹA1A2=B1B2=C1C2=D1D2=$\frac{1}{3}$A1B2���������ι��ɼ�����ȥ����������AnBnCnDn�����Ϊ$\frac{{5}^{n}}{{9}^{n}}{a}^{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ABCDE��������Σ�AP��AQ��AR����A��CD��CB��DE���ӳ����������Ĵ��ߣ���O��������ε����ģ���OP=1����AO+AQ+AR���ڣ�������
��ͼ��ABCDE��������Σ�AP��AQ��AR����A��CD��CB��DE���ӳ����������Ĵ��ߣ���O��������ε����ģ���OP=1����AO+AQ+AR���ڣ�������| A�� | 3 | B�� | 1+$\sqrt{5}$ | C�� | 4 | D�� | 2+$\sqrt{5}$ | ||||
| E�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
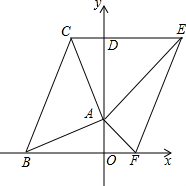 ��ͼ��������A������ֱ��AB��AE��AF�����ǵĽ���ʽ�ֱ���y=k��x+4����y=x+b��y=b-x��ֱ��AB��AF�ֱ��x�ύ��B��F���پ�����A��AB�Ĵ���AC��������D��0��4+4k���Һ�y�ᴹֱ��ֱ�߽�ֱ��AC�ڵ�C����ֱ��AE���ڵ�E��
��ͼ��������A������ֱ��AB��AE��AF�����ǵĽ���ʽ�ֱ���y=k��x+4����y=x+b��y=b-x��ֱ��AB��AF�ֱ��x�ύ��B��F���پ�����A��AB�Ĵ���AC��������D��0��4+4k���Һ�y�ᴹֱ��ֱ�߽�ֱ��AC�ڵ�C����ֱ��AE���ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
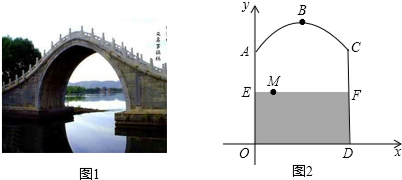
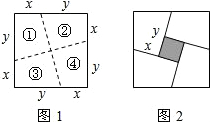 ��ͼ1������������ͼ�����ߣ�����x��y�����ɢ٢ڢۢ��Ŀ�ͼ�Σ������Ŀ�ͼ��ǡ����ƴ��һ���ı��Σ�
��ͼ1������������ͼ�����ߣ�����x��y�����ɢ٢ڢۢ��Ŀ�ͼ�Σ������Ŀ�ͼ��ǡ����ƴ��һ���ı��Σ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com