
 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=$\frac{1}{3}$A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为$\frac{{5}^{n}}{{9}^{n}}{a}^{2}$.
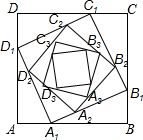
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=$\frac{1}{3}$A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为$\frac{{5}^{n}}{{9}^{n}}{a}^{2}$. 分析 首先在Rt△A1BB1中,由勾股定理可求得正方形A1B1C1D1的面积=$\frac{5}{9}{a}^{2}$,然后再在Rt△A2B1B2中,由勾股定理求得正方形A2B2C2D2的面积=$(\frac{5}{9})^{2}{a}^{2}$,然后找出其中的规律根据发现的规律即可得出结论.
解答 解:在Rt△A1BB1中,由勾股定理可知;${A}_{1}{{B}_{1}}^{2}={A}_{1}{B}^{2}+{B}_{1}{B}^{2}$=$(\frac{2}{3}a)^{2}+(\frac{1}{3}a)^{2}$=$\frac{5}{9}{a}^{2}$,即正方形A1B1C1D1的面积=$\frac{5}{9}{a}^{2}$;
在Rt△A2B1B2中,由勾股定理可知:${A}_{2}{{B}_{2}}^{2}={A}_{2}{{B}_{1}}^{2}+{B}_{2}{{B}_{1}}^{2}$=$(\frac{2}{3}×\frac{\sqrt{5}}{3}a)^{2}+(\frac{1}{3}×\frac{\sqrt{5}}{3}a)^{2}$=$(\frac{5}{9})^{2}{a}^{2}$;即正方形A2B2C2D2的面积=$(\frac{5}{9})^{2}{a}^{2}$
…
∴正方形AnBnCnDn的面积=$(\frac{5}{9})^{n}{a}^{2}=\frac{{5}^{n}}{{9}^{n}}{a}^{2}$.
故答案为:$\frac{{5}^{n}}{{9}^{n}}{a}^{2}$.
点评 本题主要考查的是正方形的性质和勾股定理的应用,通过计算发现其中的规律是解题的关键.


科目:初中数学 来源: 题型:解答题
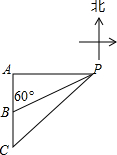 如图,已知一艘船以每小时20海里的速度向正南行驶,上午10时在A处见灯塔P在正东,1小时后行至B处,观察灯塔P的方向是北60°东,求正午12时船行驶至C处距灯塔P的距离.(答案可带根号)
如图,已知一艘船以每小时20海里的速度向正南行驶,上午10时在A处见灯塔P在正东,1小时后行至B处,观察灯塔P的方向是北60°东,求正午12时船行驶至C处距灯塔P的距离.(答案可带根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
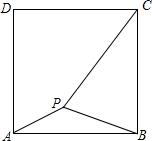 如图,正方形ABCD内有一点P,连接AP,BP,CP,若AP=1,BP=2,CP=3.
如图,正方形ABCD内有一点P,连接AP,BP,CP,若AP=1,BP=2,CP=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com