
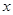 s,△PAQ的面积为
s,△PAQ的面积为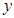 ㎝2.(这里我们把线段的面积看作是0)
㎝2.(这里我们把线段的面积看作是0)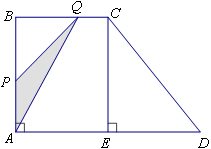
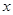 =2s时,
=2s时,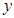 = ㎝2,当
= ㎝2,当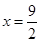 s时,
s时,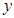 = ㎝2;
= ㎝2;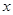 ≤14时,求
≤14时,求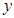 与
与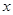 之间的函数关系式;
之间的函数关系式;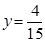
 梯形ABCD时
梯形ABCD时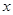 的值;
的值;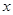 的值.
的值.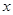 ≤9时,
≤9时, ,当9<
,当9<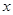 ≤13时,
≤13时, ,当13<
,当13<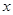 ≤14时,
≤14时, ;(3)
;(3)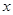 =7;(4)
=7;(4)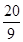 ,
, ,
,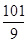 .
.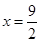 s时,三角形PAQ的高就是4,底为4.5,由三角形的面积公式可以求出其解.
s时,三角形PAQ的高就是4,底为4.5,由三角形的面积公式可以求出其解.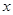 ≤14 时,求y与x之间的函数关系式.要分为三种不同的情况进行表示:当5≤
≤14 时,求y与x之间的函数关系式.要分为三种不同的情况进行表示:当5≤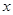 ≤9时,当9<
≤9时,当9<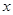 ≤13时,当13<
≤13时,当13<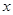 ≤14时.
≤14时.

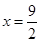 s时,AP=4.5,Q点在EC上
s时,AP=4.5,Q点在EC上 ;
;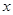 ≤9时
≤9时 (5+x-4)×4-
(5+x-4)×4- ×5(x-5)-
×5(x-5)- (9-x)(x-4)
(9-x)(x-4)
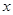 ≤13时
≤13时
 (x-9+4)(14-x)
(x-9+4)(14-x)
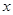 ≤14时
≤14时 ×8(14-x)
×8(14-x) ;
;
 S梯形ABCD=
S梯形ABCD= ×
× (4+8)×5=8
(4+8)×5=8 x2-7x+
x2-7x+ ,即x2-14x+49=0,解得:x1=x2=7
,即x2-14x+49=0,解得:x1=x2=7 S梯形ABCD
S梯形ABCD ,即
,即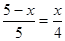 ,
, ;
; ,即
,即 ,
, ;
; ,即
,即 ,
,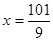 .
.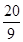 ,
, ,
,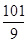 .
.

科目:初中数学 来源:不详 题型:单选题
| A.4; | B.6; | C.8; | D.10. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com