
| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |
分析 根据题意得出有三种情况:①正方形对角线交点,②画出图形,结合图形得出结论,③和②类似得出符合条件的四个点,即可得出答案.
解答 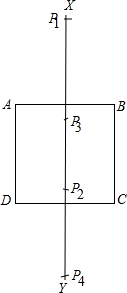 解:分为三种情况:①正方形对角线的交点;
解:分为三种情况:①正方形对角线的交点;
②作AB的垂直平分线XY,
以B为圆心,以BC为半径画弧,交XY于P1,P2,以C为圆心,以BC为半径画弧,交XY于P3,P4,
③同理作AD的垂直平分线,
以B为圆心,以AD为半径画弧,交AB的垂直平分线于两点,以A为圆心,以AD为半径画弧,交AB的垂直平分线于两点,
即共1+4+4=9个点;
故选C.
点评 本题考查了正方形性质和等腰三角形的判定,主要考查学生的理解能力和动手操作能力,熟练掌握等腰三角形的判定定理是解题的关键.


科目:初中数学 来源: 题型:解答题
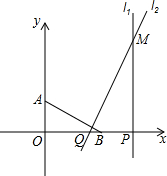 如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒
如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
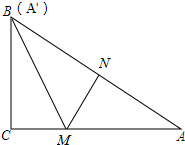 如图,在Rt△ABC中,∠ACB=90°,点M在边AC上,过点M作MN⊥AB与点N,将△MNA沿着MN折叠,恰好点A的对应点A′与点B重合.
如图,在Rt△ABC中,∠ACB=90°,点M在边AC上,过点M作MN⊥AB与点N,将△MNA沿着MN折叠,恰好点A的对应点A′与点B重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| a | -7 | b | -4 | c | d | e | f | 2 | … |
| A. | -7 | B. | -4 | C. | 4 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com