
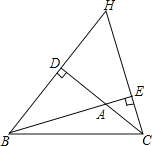
【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)如图,①在图中找出与∠DBA相等的角,并说明理由;
②若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中,∠A=50°,直接写出∠DHE的度数是 .
【答案】(1)①∠DBA=∠ECA,证明见解析;②80°;(2)50°或130°.
【解析】试题分析:(1)①根据同角的余角的相等即可说明∠DBA=∠ECA,根据四边形的内角和是360°,求得∠DHE的度数;
(2)分△ABC是锐角三角形,钝角三角形两种情况讨论求解即可.
(1)①∠DBA=∠ECA.
证明:∵BD、CE是△ABC的两条高,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠BAD=∠ECA+∠EAC=90°,
又∵∠BAD=∠EAC,
∴∠DBA=∠ECA;
②∵BD、CE是△ABC的两条高
∴∠HDA=∠HEA=90°
在四边形ADHE中,∠DAE+∠HDA+∠DHE+∠HEA=360°
又∵∠HDA=∠HEA=90°,∠DAE=∠BAC=100°
∴∠DHE=360°-90°-90°-100°=80°
(2)①△ABC是锐角三角形时,∠DHE=180°-50°=130°;
②△ABC是钝角三角形时,∠DHE=∠A=50°;
故答案为:50°或130°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
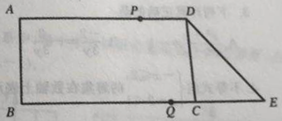
【题目】如图,在平行四边形ABCD中,∠B=90°,且AD=9cm,AB=4cm,延长BC到点E,使CE=3cm,连接DE.若动点P从A点出发,以每秒2cm的速度沿线段AD运动;动点Q从E点出发以每秒3cm的速度沿EB向B点运动,当点P、Q有一个到位置时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
(1)求DE的长
(2)当t为多少时,四边形PQED成为平行四边形;
(3)请直接写出使得△DQE是等腰三角形时t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一次函数y=kx+b的图象,以下说法中正确的是( )

A. 直线与y轴的交点为(3,0) B. y随x的增大而增大
C. 直线与两坐标轴围成的三角形面积是6 D. 一元一次方程kx+b=0的解为x=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.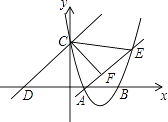
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE , 现给出下列命题:①若 ![]() =
= ![]() ,则tan∠EDF=
,则tan∠EDF= ![]() ;②若DE2=BDEF,则DF=2AD,则( )
;②若DE2=BDEF,则DF=2AD,则( ) 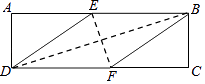
A.①是假命题,②是假命题
B.①是真命题,②是假命题
C.①是假命题,②是真命题
D.①是真命题,②是真命题
查看答案和解析>>
科目:初中数学 来源: 题型:
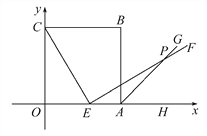
【题目】如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
(1)求证:CE=EP.
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将二次函数y=x2﹣m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1 , 另有一次函数y=x+b的图象记为y2 , 则以下说法: ①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m< ![]() ;
;
③当m=﹣b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为 . 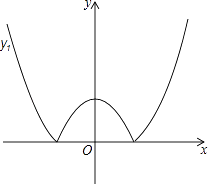
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点.观察图象可知:当x=﹣3或1时,y1=y2 .
交于A(1,3)和B(﹣3,﹣1)两点.观察图象可知:当x=﹣3或1时,y1=y2 . 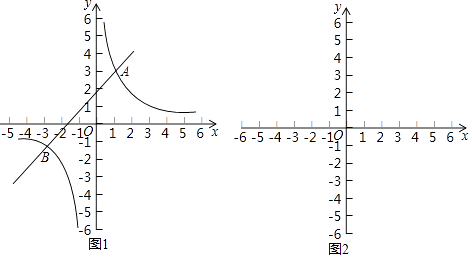
(1)通过观察函数的图象,可以得到不等式ax+b> ![]() 的解集 .
的解集 .
(2)参考观察函数的图象方法,解决问题:关于x的不等式x2+a﹣ ![]() <0(a>0)只有一个整数解,则a的取值范围 .
<0(a>0)只有一个整数解,则a的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com