
【题目】已知:∠AOB= ![]() °,过点O作OB⊥OC.请画图示意并求解.
°,过点O作OB⊥OC.请画图示意并求解.
(1)若 ![]() =30,则∠AOC=________.
=30,则∠AOC=________.
(2)若 ![]() =40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
=40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
(3)若0< ![]() <180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=________°.(用
<180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=________°.(用 ![]() 的代数式表示).
的代数式表示).
【答案】(1)120°或60°(2)示意图详见解析,20°;(3)![]() .
.
【解析】
(1)由OB⊥OC可得出∠BOC=90°,分射线OA、OC在射线OB同侧和两侧讨论,结合图形即可得出结论;
(2)分射线OA、OC在射线OB同侧和两侧讨论,根据角平分线定义即可得出∠COE和∠COF的大小,结合图形即可求出∠EOF的度数;
(3)分射线OA、OC在射线OB同侧和两侧讨论,根据角平分线定义即可得出∠COE和∠COF的大小,结合图形即可求出∠EOF的度数.
根据题意画出图形,如图所示.
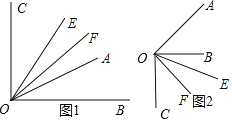
(1)∵OB⊥OC,
∴∠BOC=90°.
当射线OA、OC在射线OB同侧时,∠AOC=∠BOC-∠AOB=60°;
当射线OA、OC在射线OB两侧时,∠AOC=∠AOB+∠BOC=120°.
故答案为:60°或120°.
(2)当射线OA、OC在射线OB同侧时,
∵射线OE平分∠AOC,射线OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (∠BOC-∠AOB)=
(∠BOC-∠AOB)=![]() ×(90°-40°)=25°,∠COF=
×(90°-40°)=25°,∠COF=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠COF-∠COE=45°-25°=20°;
当射线OA、OC在射线OB两侧时,
∵射线OE平分∠AOC,射线OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOB)=
(∠BOC+∠AOB)=![]() ×(90°+40°)=65°,∠COF=
×(90°+40°)=65°,∠COF=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠COE-∠COF=65°-45°=20°.
综上可知:∠EOF的度数为20°.
(3)当射线OA、OC在射线OB同侧时,
∵射线OE平分∠AOC,射线OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (∠BOC-∠AOB)=
(∠BOC-∠AOB)=![]() ×(90°-α°)=45°-
×(90°-α°)=45°-![]() °,∠COF=
°,∠COF=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠COF-∠COE=45°-(45°-![]() °)=
°)=![]() °;
°;
当射线OA、OC在射线OB两侧时,
∵射线OE平分∠AOC,射线OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOB)=
(∠BOC+∠AOB)=![]() ×(90°+α°)=45°+
×(90°+α°)=45°+![]() °,∠COF=
°,∠COF=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠COE-∠COF=(45°+![]() °)-45°=
°)-45°=![]() .
.
故答案为:![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏中奖的概率是 ![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差S甲2=0.2,乙组数据的方差S乙2=0.5,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市某月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市,并连续停留3天.则此人在该市停留期间有且仅有1天空气质量重度污染的概率是( )
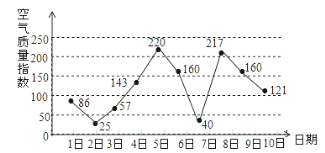
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB= ![]() ,BC=
,BC= ![]() .
.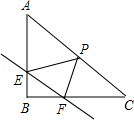
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题
如图,在6×6的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.

(1)从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为![]() ;
;
(2)以(1)中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数;
(3)画出△ABC关于点B的中心对称图形△A1B1C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在进行二次根式化简时,我们有时会碰上如![]() ,
,![]() ,
, ![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简:
![]() =
=![]() (一),
(一),
![]() (二),
(二),
 (三),
(三),
![]() 还可以用以下方法化简:
还可以用以下方法化简: ![]() =
= (四)
(四)
以上这种化简的方法叫做分母有理化。
(1)请化简![]() =___.
=___.
(2)若a是![]() 的小数部分则
的小数部分则![]() =___.
=___.
(3)矩形的面积为![]() ,一边长为
,一边长为![]() ,则它的周长为___.
,则它的周长为___.
(4)化简![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数![]() ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行.某自行车厂生产的某型号自行车去年销售总额为8万元.今年该型号自行车每辆售价预计比去年降低200元.若该型号车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求该型号自行车去年每辆售价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com