
【题目】计算:
(1)﹣20+(﹣14)﹣(﹣18)﹣13 (2)27-18+43-32
(3)(+![]() )﹣(﹣
)﹣(﹣![]() )﹣|﹣3| (4)
)﹣|﹣3| (4)![]()
(5)﹣64÷3![]() ×
×![]() ; (6)∣-2∣
; (6)∣-2∣![]() 2+∣+7∣
2+∣+7∣![]() 7+∣0∣
7+∣0∣
(7)![]() (8)
(8) ![]()
【答案】(1) -29;(2)20;(3)-1;(4)6;(5)-12.5;(6)5;(7)-7;(8)-1799.5
【解析】
(1)原式利用减法法则变形,计算即可得到结果.
(3)(6)原式先计算绝对值运算,再计算乘除加减运算即可得到结果.
(4)(5)原式先计算乘除,再加减运算即可得到结果.
(2)原式从左到右依次计算即可得到结果.
(7)原式利用乘法分配律计算即可得到结果分析.
(8)先变式再利用乘法分配律计算即可得到结果.
(1)﹣20+(﹣14)﹣(﹣18)﹣13=-20-14+18-13=-29.
(2)27-18+43-32 =20.
(3)(+![]() )﹣(﹣
)﹣(﹣![]() )﹣|﹣3|=
)﹣|﹣3|=![]() -3=-1
-3=-1
(4)![]() =6
=6
(5)﹣64÷3![]() ×
×![]() =
=![]() = -12.5
= -12.5
(6)![]() =4+1+0=5
=4+1+0=5
(7)![]() =—(-18)
=—(-18)![]() =-7
=-7
(8) ![]() =
=![]() =-1800+0.5=-1799.5
=-1800+0.5=-1799.5


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= ![]() 的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
A.1
B.﹣5
C.4
D.1或﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
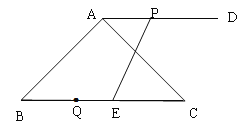
【题目】如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10 cm,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1cm的速度运动,同时点Q从点C出发沿射线CB方向以每秒2cm的速度运动,在线段QC上取点E,使得QE =2cm,连结PE,设点P的运动时间为t秒.
(1)①CE= (用含t的式子表示)
②若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了更好地活跃校园文化生活,拟对本校自办的“辉煌”校报进行改版.先从全校学生中随机抽取一部分学生进行了一次问卷调查,题目为“你最喜爱校报的哪一个板块”(每人只限选一项).问卷收集整理后绘制了不完整的频数分布表和如图扇形统计图.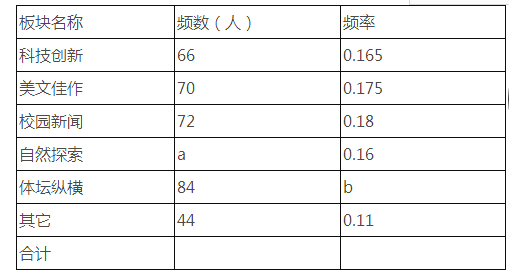
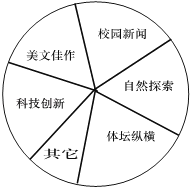
(1)填空:频数分布表中a= , b=;
(2)“自然探索”板块在扇形统计图中所占的圆心角的度数为;
(3)在参加此次问卷调查的学生中,最喜爱哪一个板块的人数最多?有多少人喜欢?
(4)若全校有1500人,估计喜欢“校园新闻”板块的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是AC边上一点,AD=10,DC=8.以AD为直径的⊙O与边BC切于点E,且AB=BE
(1)求证:AB是⊙O的切线;
(2)过D点作DF∥BC交⊙O于点F,求线段DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c<0;③ac>0;④b2﹣4ac>0.其中正确的结论是( )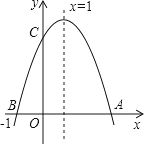
A.①④
B.①③
C.②④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个不透明的乒乓球盒,甲盒中装有1个白球和2个红球,乙盒中装有2个白球和若干个红球,这些小球除颜色不同外,其余均相同.若从乙盒中随机摸出一个球,摸到红球的概率为 ![]() .
.
(1)求乙盒中红球的个数;
(2)若先从甲盒中随机摸出一个球,再从乙盒中随机摸出一个球,请用树形图或列表法求两次摸到不同颜色的球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某实验学校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
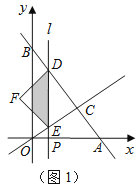
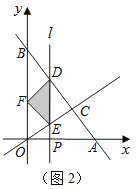
【题目】如图1,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,
交于点C(2,![]() ).平行于
).平行于![]() 轴的直线l从原点O出发,以每秒1个单位长度的速度沿
轴的直线l从原点O出发,以每秒1个单位长度的速度沿![]() 轴向右平移,到C点时停止;直线l分别交线段BC、OC、
轴向右平移,到C点时停止;直线l分别交线段BC、OC、![]() 轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为
轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为![]() (秒).
(秒).
(1)求![]() 、
、![]() 的值;
的值;
(2)当![]() 为何值时,点F在
为何值时,点F在![]() 轴上(如图2);
轴上(如图2);
(3)设△DEF与△BCO重叠部分的面积为S,请求出S与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com