
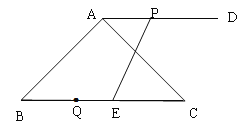
【题目】如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10 cm,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1cm的速度运动,同时点Q从点C出发沿射线CB方向以每秒2cm的速度运动,在线段QC上取点E,使得QE =2cm,连结PE,设点P的运动时间为t秒.
(1)①CE= (用含t的式子表示)
②若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由。
【答案】(1)①CE=2t -2②![]() (2)存在,t=4或12s
(2)存在,t=4或12s
【解析】分析:(1)作AM⊥BC于M,由已知条件得出AB=AC,由等腰三角形的性质得出BM=CM,由直角三角形斜边上的中线性质得出AM=![]() BC=5,证出△APN和△CEN是等腰直角三角形,得出PN=AP=t,CE=NE=5-t,由CE=CQ-QE=2t-2得出方程,解方程即可;
BC=5,证出△APN和△CEN是等腰直角三角形,得出PN=AP=t,CE=NE=5-t,由CE=CQ-QE=2t-2得出方程,解方程即可;
(2)由平行四边形的判定得出AP=BE,分类讨论得出方程,解方程即可.
详解:(1)①CE= 2t -2(用含t的式子表示)
②作AM⊥BC于M,如图所示:
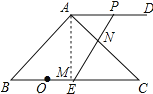
∵∠BAC=90°,∠B=45°,
∴∠C=45°=∠B,
∴AB=AC,
∴BM=CM,
∴![]()
∵AD∥BC,
∴∠PAN=∠C=45°,
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5-t,
∵CE=CQ-QE=2t-2,
∴5-t=2t-2,
解得: ![]() ;
;
(2)存在,t=4或12s;理由如下:
(ⅰ)当点Q、E在线段BC上时,
若以A,B,E,P为顶点的四边形为平行四边形,
则AP=BE,
∴t=10-2t+2,
解得:t=4,
(ⅱ)当点Q、E在线段CB的延长线上时,
若以A,B,E,P为顶点的四边形为平行四边形
则AP=BE,
t=2t-2-10
解得:t=12
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12 s。


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
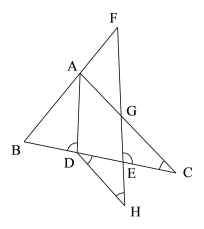
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,AD∥EF.
(1)求证:∠BDA+∠CEG=180°;
(2)若点H在FE的延长线上,且∠F=∠H,则∠EDH与∠C相等吗,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
(1)“快车”行驶里程不超过5公里计费8元;
(2)“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
(3)A点的坐标为(6.5,10.4);
(4)从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧 ![]() 上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.
上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.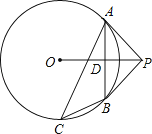
(1)求证:PB为⊙O的切线;
(2)若tan∠BCA= ![]() ,⊙O的半径为
,⊙O的半径为 ![]() ,求弦AB的长.
,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③![]() ;
;
④四边形ABCD是矩形.其中说法正确的有( )
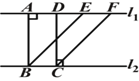
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
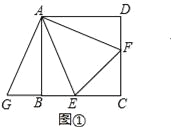
【题目】如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为 . 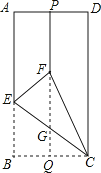
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣20+(﹣14)﹣(﹣18)﹣13 (2)27-18+43-32
(3)(+![]() )﹣(﹣
)﹣(﹣![]() )﹣|﹣3| (4)
)﹣|﹣3| (4)![]()
(5)﹣64÷3![]() ×
×![]() ; (6)∣-2∣
; (6)∣-2∣![]() 2+∣+7∣
2+∣+7∣![]() 7+∣0∣
7+∣0∣
(7)![]() (8)
(8) ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com