
【题目】某校七年级组织数学嘉年华活动,共评出三个奖项,年级处购买了一些奖品进行表彰,相关统计结果如下表(不完整)所示:
一等奖 | 二等奖 | 三等奖 | 合计 | |
获奖人数(单位:人) | 40 | |||
奖品单价(单位:元) | 12 | 9 | 6 | |
奖品金额(单位:元) | 300 |
已知二等奖的获奖人数比一等奖的获奖人数多5人.你能根据所给条件,分别求出三种奖项的获奖人数吗?请根据你所设的未知数,先填表(代数式不必化简),再列方程解答.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
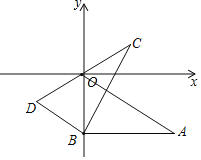
【题目】Rt△ABO与Rt△CBD在平面直角坐标系中的位置如图所示,∠ABO=∠CBD=90°,若点A(2![]() ,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )
,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )
A. (2,2![]() )B. (1,
)B. (1,![]() )C. (
)C. (![]() ,1)D. (2
,1)D. (2![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2016个正整数1、2、3、4、……、2016按如图方式排列成一个表,用一方框按如图所示的方式任意框住9个数.(方框只能平移)
(1)若框住的9个数中,正中间的一个数为39,则:这九个数的和为__________.
(2)方框能否框住这样的9个数,它们的和等于2016?若能,请写出这9个数;若不能,请说明理由。
(3)若任意框住9个数的和记为S,则:S的最大值与最小值之差等于__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
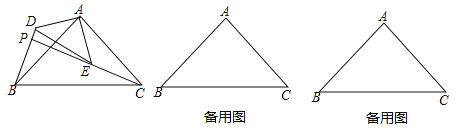
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
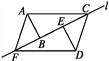
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
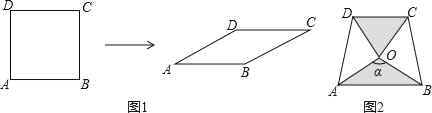
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
(1)请补全表:
α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
S |
| 1 |
|
(2)填空:
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=![]() ;当α=135°时,S=S(135°)=
;当α=135°时,S=S(135°)=![]() .由上表可以得到S(60°)=S( °);S(150°)=S( °),…,由此可以归纳出S(180°﹣α)=( °).
.由上表可以得到S(60°)=S( °);S(150°)=S( °),…,由此可以归纳出S(180°﹣α)=( °).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
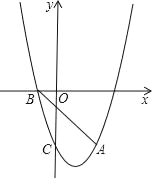
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com