
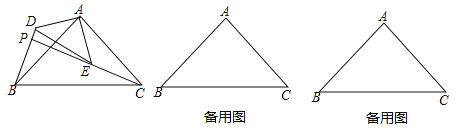
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;
【答案】(1)证明见解析;(2)PB的长为![]() 或
或![]() .
.
【解析】试题分析:(1)依据等腰三角形的性质得到AB=AC,AD=AE,依据同角的余角相等得到∠DAB=∠CAE,然后依据SAS可证明△ADB≌△AEC,最后,依据全等三角形的性质可得到BD=CE;
(2)分为点E在AB上和点E在AB的延长线上两种情况画出图形,然后再证明△PEB∽△AEC,最后依据相似三角形的性质进行证明即可.
试题解析:解:(1)∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠DAB=∠CAE,∴△ADB≌△AEC,∴BD=CE.
(2)解:①当点E在AB上时,BE=AB﹣AE=1.
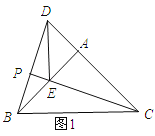
∵∠EAC=90°,∴CE=![]() =
=![]() .
.
同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA.
∵∠PEB=∠AEC,∴△PEB∽△AEC,∴![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() .
.
②当点E在BA延长线上时,BE=3.
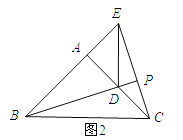
∵∠EAC=90°,∴CE=![]() =
=![]() .
.
同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA.
∵∠BEP=∠CEA,∴△PEB∽△AEC,∴![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() .
.
综上所述,PB的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某景区的门票销售分两类:一类为散客门票,价格为![]() 元/张;另一类为团体门票(一次性购买门票
元/张;另一类为团体门票(一次性购买门票![]() 张以上),每张门票价格在散客门票价格的基础上打
张以上),每张门票价格在散客门票价格的基础上打![]() 折,某班部分同学要去该景点旅游,设参加旅游
折,某班部分同学要去该景点旅游,设参加旅游![]() 人,购买门票需要
人,购买门票需要![]() 元
元
(1)如果每人分别买票,求![]() 与
与![]() 之间的函数关系式:
之间的函数关系式:
(2)如果购买团体票,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(3)请根据人数变化设计一种比较省钱的购票方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,![]() D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且![]() 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF

(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级组织数学嘉年华活动,共评出三个奖项,年级处购买了一些奖品进行表彰,相关统计结果如下表(不完整)所示:
一等奖 | 二等奖 | 三等奖 | 合计 | |
获奖人数(单位:人) | 40 | |||
奖品单价(单位:元) | 12 | 9 | 6 | |
奖品金额(单位:元) | 300 |
已知二等奖的获奖人数比一等奖的获奖人数多5人.你能根据所给条件,分别求出三种奖项的获奖人数吗?请根据你所设的未知数,先填表(代数式不必化简),再列方程解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
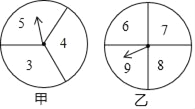
【题目】在一次数学兴趣小组活动中,小明和小红两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则小明获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则小红获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出小明和小红获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
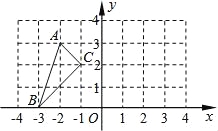
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按下列方式搭建三角形:
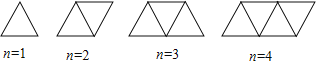
(1)当三角形个数为1时,需3根火柴棒;当三角形个数为2时,需5根火柴棒;则当三角形个数为100时,需火柴棒 根;当三角形个数为n时,需火柴棒 根(用含n的代数式表示);
(2)当火柴棒的根数为2019时,求三角形的个数?
(3)组成三角形的火柴棒能否为1000根,如果能,求三角形的个数;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com