
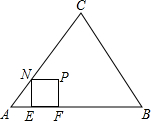
 如图,正三角形ABC的边长为2$\sqrt{3}$.
如图,正三角形ABC的边长为2$\sqrt{3}$.分析 (1)利用位似图形的性质,作出正方形EFPN的位似正方形E′F′P′N′,如答图①所示;
(2)根据正三角形、正方形、直角三角形相关线段之间的关系,利用等式E′F′+AE′+BF′=AB,列方程求得正方形E′F′P′N′的边长.
解答 解:(1)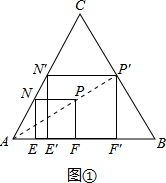 如图①,正方形E′F′P′N′即为所求.
如图①,正方形E′F′P′N′即为所求.
(2)设正方形E′F′P′N′的边长为x,
∵△ABC为正三角形,
∴AE′=BF′=$\frac{\sqrt{3}}{3}$x.
∵E′F′+AE′+BF′=AB,
∴x+$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$x=2$\sqrt{3}$,
解得:x=12-6$\sqrt{3}$.
故正方形E′F′P′N′的边长为12-6$\sqrt{3}$..
点评 本题考查了位似变换、正三角形、正方形、直角三角形边角性质等知识,利用等边三角形的性质表示出AE′,BF′的长是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC与△ABD中,AD与BC相交于0点,∠1=∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC=BD.并给出证明.
如图,在△ABC与△ABD中,AD与BC相交于0点,∠1=∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC=BD.并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )

A. 4 B. 3 C. 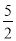 D. 2
D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com