
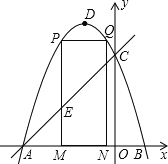
【题目】如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)设点H是第二象限内抛物线上的一点,且△HAB的面积是6,求点H的坐标;
(3)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积.
【答案】(1)A(-3,0),B(1,0),C(0,3);(2)H(-2,3);(3)![]() .
.
【解析】
试题分析:(1)通过解析式即可得出C点坐标,令y=0,解方程得出方程的解,即可求得A、B的坐标.
(2)根据AB的长和三角形面积求得H的纵坐标为3,代入解析式即可求得横坐标;
(3)设M点横坐标为m,则PM=-m2-2m+3,MN=(-m-1)×2=-2m-2,矩形PMNQ的周长d=-2m2-8m+2,将-2m2-8m+2配方,根据二次函数的性质,即可得出m的值,然后求得直线AC的解析式,把x=m代入可以求得三角形的边长,从而求得三角形的面积.
试题解析:(1)由抛物线y=-x2-2x+3可知,C(0,3),
令y=0,则0=-x2-2x+3,解得x=-3或x=1,
∴A(-3,0),B(1,0).
(2)∵A(-3,0),B(1,0).
∴AB=4,
∵△HAB的面积是6,点H是第二象限内抛物线上的一点,
∴H的纵坐标为3,
把y=3代入y=-x2-2x+3得3=-x2-2x+3,解得x1=0,x2=-2,
∴H(-2,3);
(3)由抛物线y=-x2-2x+3可知,对称轴为x=-1,
设M点的横坐标为m,则PM=-m2-2m+3,MN=(-m-1)×2=-2m-2,
∴矩形PMNQ的周长=2(PM+MN)=(-m2-2m+3-2m-2)×2=-2m2-8m+2=-2(m+2)2+10,
∴当m=-2时矩形的周长最大.
∵A(-3,0),C(0,3),设直线AC解析式为y=kx+b,
则![]() 解得:
解得:![]() ,
,
∴解析式y=x+3,当x=-2时,则E(-2,1),
∴EM=1,AM=1,
∴S=![]() ×AM×EM=
×AM×EM=![]() .
.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D, DE⊥AB于点E,DF⊥AC于F.连接DB、DC
(1)求证:△DBE≌△DFC.
(2)求证:AB+AC=2AE
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D, DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系。(不需证明,只需在图2中作出辅助线、说明证哪两个三角形全等即可)。
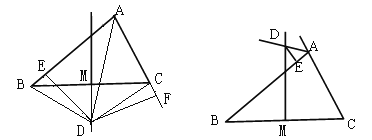
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】幼儿园的小朋友打算选择一种形状、大小都相同的多边形塑料胶板铺地面.为了保证铺地时既无缝隙,又不重叠,请你告诉他们可以选择哪些形状的塑料胶板(填三种) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,已知:
如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴ = ( ).
同理可得,PB= .
∴ = (等量代换).
∴ (到一条线段两个端点距离相等的点,在这条线段的 )
∴AB、BC、AC的垂直平分线 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.以其中三个条件为题设,填入已知栏中,一个论断为结论,填入下面求证栏中,使之组成一个真命题,并写出证明过程.
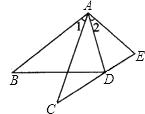
已知: .
求证: .
证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com