
【题目】如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D, DE⊥AB于点E,DF⊥AC于F.连接DB、DC
(1)求证:△DBE≌△DFC.
(2)求证:AB+AC=2AE
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D, DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系。(不需证明,只需在图2中作出辅助线、说明证哪两个三角形全等即可)。
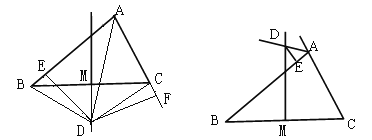
图1 图2
【答案】(1)见解析(2)见解析(3)BE=AE+AC
【解析】试题分析:(1)根据线段垂直平分线的性质得到DB=DC,根据角平分线的性质得到DE=DF,由全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AE=AF,BE=CF,等量代换即可得到结论;
(3)如图2,过D作DN⊥AC,垂足为N,连接DB、DC,根据线段垂直平分线的性质和角平分线的性质得到DN=DE,DB=DC,推出Rt△DBE≌Rt△DCN(HL),根据全等三角形的性质得到BE=CN,由于Rt△DEA≌Rt△DNA(HL),根据全等三角形的性质得到AN=AE,等量代换即可得到结论.
(1)证明:∵DM垂直平分BC,
∴DB=DC,
∵∠1=∠2,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△DEB与Rt△DFC中,
![]() ,
,
∴Rt△DEB≌Rt△DFC;
(2)∵∠AED=∠AFD=90°,
在Rt△ADE≌Rt△ADF中,
![]() ,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
又∵Rt△DEB≌Rt△DFC,
∴BE=CF,
∴AB+AC=AE+BE+AF﹣CF=2AE;
(3)BE=AE+AC.
证明:如图2,过D作DN⊥AC,垂足为N,连接DB、DC,
则DN=DE,DB=DC,
又∵DE⊥AB,DN⊥AC,
∴∠DEB=∠DNC=90°,
在Rt△DBE和Rt△DCN中,
![]() ,
,
∴Rt△DBE≌Rt△DCN(HL)
∴BE=CN,
在Rt△DEA和Rt△DNA中,
![]() ,
,
∴Rt△DEA≌Rt△DNA(HL),
∴AN=AE,
∴BE=AC+AN=AC+AE,
即BE=AE+AC.


科目:初中数学 来源: 题型:
【题目】已知A(﹣2,a),B(1,b)是一次函数y=﹣2x+3的图象上的两个点,则a与b的大小关系是( )
A. a>bB. a<bC. a=bD. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
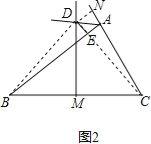
【题目】如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的坐标为 ( )
A. 8065 B. 8064 C. 8063 D. 8062
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.13cm B.14cm C.13cm或14cm D.以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
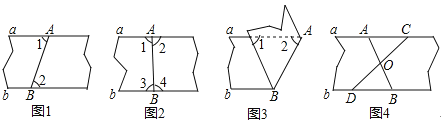
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=r2,则称点P′是点P关于⊙O的“反演点”.

如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
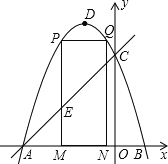
(1)求A、B、C的坐标;
(2)设点H是第二象限内抛物线上的一点,且△HAB的面积是6,求点H的坐标;
(3)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com