
【题目】如图,在边长为![]() 正方形
正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一动点(不包括两个端点),连接
上一动点(不包括两个端点),连接![]() .
.
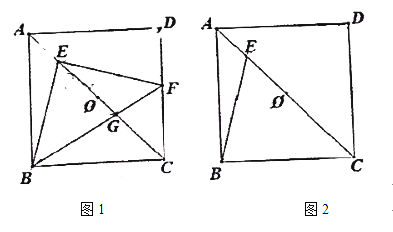
(1)如图1,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
①求证:![]() ;
;
②设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(2)在如图2中,请用无刻度的直尺作出一个以![]() 为边的菱形.
为边的菱形.
【答案】(1)①见解析;②![]() ;(2)见解析
;(2)见解析
【解析】
(1)①连接DE,如图1,先用SAS证明△CBE≌△CDE,得EB=ED,∠CBE=∠1,再用四边形的内角和可证明∠EBC=∠2,从而可得∠1=∠2,进一步即可证得结论;
②将△BAE绕点B顺时针旋转90°,点E落在点P处,如图2,用SAS可证△PBG≌△EBG,所以PG=EG=2-x-y,在直角三角形PCG中,根据勾股定理整理即得y与x的函数关系式,再根据题意写出x的取值范围即可.
(2)由(1)题已得EB=ED,根据正方形的对称性只需再确定点E关于点O的对称点即可,考虑到只有直尺,可延长![]() 交AD于点M,再连接MO并延长交BC于点N,再连接DN交AC于点Q,问题即得解决.
交AD于点M,再连接MO并延长交BC于点N,再连接DN交AC于点Q,问题即得解决.
(1)①证明:如图1,连接DE,∵四边形ABCD是正方形,
∴CB=CD,∠BCE=∠DCE=45°,
又∵CE=CE,∴△CBE≌△CDE(SAS),
∴EB=ED,∠CBE=∠1,
∵∠BEC=90°,∠BCF=90°,
∴∠EBC+∠EFC=180°,
∵∠EFC+∠2=180°,
∴∠EBC=∠2,
∴∠1=∠2.
∴ED=EF,
∴BE=EF.
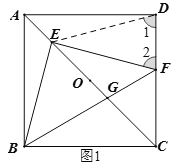
②解:∵正方形ABCD的边长为![]() ,∴对角线AC=2.
,∴对角线AC=2.
将△BAE绕点B顺时针旋转90°,点A与点C重合,点E落在点P处,如图2,
则△BAE≌△BCP,
∴BE=BP,AE=CP=x,∠BAE=∠BCP=45°,∠EBP=90°,
由①可得,∠EBF=45°,∴∠PBG=45°=∠EBG,
在△PBG与△EBG中,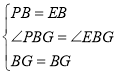 ,
,
∴△PBG≌△EBG(SAS).
∴PG=EG=2-x-y,
∵∠PCG=∠GCB+∠BCP=45°+45°=90°,
∴在Rt△PCG中,由![]() ,得
,得![]() ,
,
化简,得![]() .
.
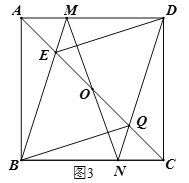
(2)如图3,作法如下:
①延长![]() 交AD于点M,
交AD于点M,
②连接MO并延长交BC于点N,
③连接DN交AC于点Q,
④连接DE、BQ,
则四边形BEDQ为菱形.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车同时从相距![]() 千米的
千米的![]() 两地沿同条公路相向而行(甲由
两地沿同条公路相向而行(甲由![]() 到
到![]() ,乙由
,乙由![]() 到
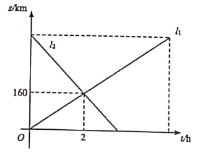
到![]() ).如图,
).如图,![]() 分别表示两辆汽车与
分别表示两辆汽车与![]() 地之间的距离
地之间的距离![]() 与行驶时间
与行驶时间![]() 之间的关系.
之间的关系.
![]() 分别求
分别求![]() 对应的函数表达式;
对应的函数表达式;
![]() 甲车到达
甲车到达![]() 地比乙车到达
地比乙车到达![]() 地多用_ 小时;
地多用_ 小时;
![]() 出发多少小时后,两车相距
出发多少小时后,两车相距![]() 千米?
千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲正在阅读《三国演义》,每天所读页数相同,当他读完第84页时,乙从头开始阅读同一本书籍,每天所读页数相同;下列表格记录了甲乙两人同读《三国演义》的进度.例如:第五天结束时,两人已读页数之和为424,此时甲比乙多读了24页;(注:已读页数中已计入了甲先读完的84页)
同读天数 | 1 | 2 | 3 | 4 | 5 |
已读页数之和 | 152 | 220 | a | b | 424 |
已读页数之差 | 72 | 60 | 48 | 36 | 24 |
(1)请直接写出表格中a、b的值;
(2)列方程求解:甲、乙两人每天各读书多少页?
(3)若这本书共有520页,从第6天起,甲每天比原来多读n页,乙每天所读页数不变,这样到第11天结束时,甲、乙两人已读页数相同,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
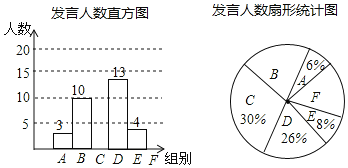
(1)直接写出随机抽取学生的人数为 人;
(2)直接补全频数直方图和扇形统计图;
(3)该校七年级共有学生1000人,请估计七年级在这天里发言次数大于等于12次的人数.
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C三点共线,线段AB=10cm,BC=16cm,点E,F分别是线段AB,BC的中点,则线段EF的长为( )
A.13cm或3cmB.13cmC.3cmD.13cm或18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的原点为0,点A、B、C是数轴上的三点,点B对应的数位1,AB=6,BC=2,动点P、Q同时从A、C出发,分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动.设运动时间为t秒(t>0)
(1)求点A、C分别对应的数;
(2)经过t秒后,求点P、Q分别对应的数(用含t的式子表示)
(3)试问当t为何值时,OP=OQ?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:
①玩家只能将小兔从A、B两个出入口放入;
②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元.
(1)问小美得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com