
【题目】我校快乐走班数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°)小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.
活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
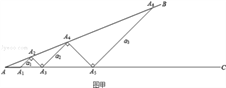
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能“或“不能”)
(2)设AA1=A1A2=A2A3=1.则θ= 度;
活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.

数学思考:
(3)若只能摆放5根小棒,求θ的范围.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
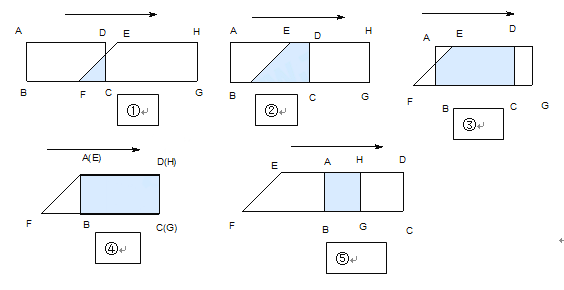
【题目】已知:如图,在矩形ABCD中,AD=6㎝,AB=3㎝。在直角梯形中EFGH中 ,EH∥FG ,∠EFG=![]() ,∠G=
,∠G=![]() ,EH=6㎝,HG=3㎝。B、C、F、G同在一条直线上。当F、C两点重合时,矩形ABCD以1㎝/秒的速度沿直线按箭头所示的方向匀速平移,
,EH=6㎝,HG=3㎝。B、C、F、G同在一条直线上。当F、C两点重合时,矩形ABCD以1㎝/秒的速度沿直线按箭头所示的方向匀速平移, ![]() 秒后,矩形ABCD与梯形EFGH重合部分的面积为
秒后,矩形ABCD与梯形EFGH重合部分的面积为![]() ㎝。按要求回答下列各题(不要求写出解题过程):
㎝。按要求回答下列各题(不要求写出解题过程):
(1)当![]() 时,
时, ![]() cm2(如图①);
cm2(如图①);
当![]() 时,
时, ![]() cm2(如图④);
cm2(如图④);
(2)在下列各种情况下,分别用![]() 表示
表示![]() :
:
如图①,当![]() 时,
时, ![]() cm2;
cm2;
如图②,当![]() 时,
时, ![]() cm2;
cm2;
如图③,当![]() 时,
时, ![]() cm2;
cm2;
如图⑤,当![]() 时,
时, ![]() cm2.
cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )

A. 4 B. 2![]() C. 2 D. 6
C. 2 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+1与反比例函数y=![]() 的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
(1)求此反比例函数的解析式;
(2)当一次函数y=x+1的值大于反比例函数y=![]() 的值时,求自变量x的取值范围.
的值时,求自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
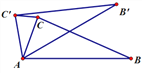
A. 70° B. 35° C. 40° D. 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com