
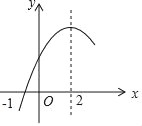
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>﹣3b;(3)7a﹣3b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】根据题意和函数的图像,可知抛物线的对称轴为直线x=-![]() =2,即b=-4a,变形为4a+b=0,所以(1)正确;
=2,即b=-4a,变形为4a+b=0,所以(1)正确;
由x=-3时,y>0,可得9a+3b+c>0,可得9a+c>-3c,故(2)正确;
因为抛物线与x轴的一个交点为(-1,0)可知a-b+c=0,而由对称轴知b=-4a,可得a+4a+c=0,即c=-5a.代入可得7a﹣3b+2c=7a+12a-5a=14a,由函数的图像开口向下,可知a<0,因此7a﹣3b+2c<0,故(3)不正确;
根据图像可知当x<2时,y随x增大而增大,当x>2时,y随x增大而减小,可知若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(7,y3)在该函数图象上,则y1=y3<y2,故(4)不正确;
,y2)、点C(7,y3)在该函数图象上,则y1=y3<y2,故(4)不正确;
根据函数的对称性可知函数与x轴的另一交点坐标为(5,0),所以若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<x2,故(5)正确.
正确的共有3个.
故选:B.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(1) 知识储备
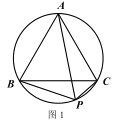
①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.
②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC
的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
(2)知识迁移
①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段____的长度即为△ABC 的费马距离.
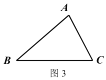
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个(__________);
ⅱ.任意三角形的费马点一定在三角形的内部(__________).
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为![]() ,求正方形 ABCD 的
,求正方形 ABCD 的
边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当矩形ABCD的长和宽满足什么条件时,四边形MENF是正方形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,BF与CE相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)①若四边形EHFG是菱形,则平行四边形ABCD必须满足条件 ;
②若四边形EHFG是矩形,则平行四边形ABCD必须满足条件 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为_____.
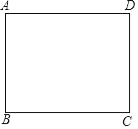
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边BC在x轴上,且∠ACB=90°.反比例函数y=![]() (x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
(x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
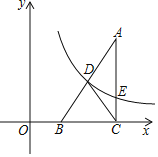
(1)求k的值;(2)若AE=BC,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化小区环境,预计花园每平方米造价为25元,小区修建这个花园需要投资多少元?
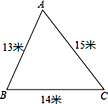
查看答案和解析>>
科目:初中数学 来源: 题型:
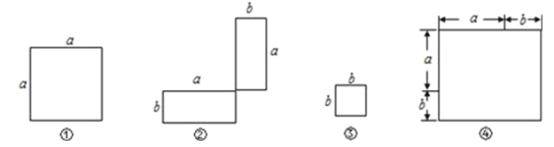
【题目】在下列横线上用含有![]() ,
,![]() 的代数式表示相应图形的面积.
的代数式表示相应图形的面积.
(1)①________;②__________;③__________;④_________________.
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:________________________________________.
(3)利用(2)的结论计算1972+2×197×3+32的值.( 注意不利用以上结论不得分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com