
【题目】如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,BF与CE相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)①若四边形EHFG是菱形,则平行四边形ABCD必须满足条件 ;
②若四边形EHFG是矩形,则平行四边形ABCD必须满足条件 .

【答案】(1)证明见解析;(2)①平行四边形ABCD是矩形;②当平行四边形ABCD是矩形,并且AB=2AD.
【解析】
(1)通过证明两组对边分别平行,可得四边形EHFG是平行四边形;
(2)①当平行四边形ABCD是矩形时,通过证明有一组邻边相等,可得平行四边形EHFG是菱形;
②当平行四边形ABCD是矩形,并且AB=2AD时,先证明四边形ADFE是正方形,得出有一个内角等于90°,从而证明菱形EHFG为一个矩形
(1)证明:∵四边形ABCD是平行四边形,
∴AE∥CF,AB=CD,
∵E是AB中点,F是CD中点,
∴AE=CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
同理可得DE∥BF,
∴四边形FGEH是平行四边形;
(2)①当平行四边形ABCD是矩形时,平行四边形EHFG是菱形.
∵四边形ABCD是矩形
∴∠ABC=∠DCB=90°,
∵E是AB中点,F是CD中点,
∴BE=CF,
在△EBC与△FCB中,
∵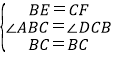 ,
,
∴△EBC≌△FCB,
∴CE=BF,
∠ECB=∠FBC,
BH=CH,
EH=FH,
平行四边形EHFG是菱形;
②解:当平行四边形ABCD是矩形,并且AB=2AD时,平行四边形EHFG是矩形.理由如下:
连接EF,如图所示:
∵E,F分别为AB,CD的中点,且AB=CD,
∴AE=DF,且AE∥DF,
∴四边形AEFD为平行四边形,
∴AD=EF,
又∵AB=2AD,E为AB中点,则AB=2AE,
于是有AE=AD=![]() AB,
AB,
这时,EF=AE=AD=DF=![]() AB,∠EAD=∠FDA=90°,
AB,∠EAD=∠FDA=90°,
∴四边形ADFE是正方形,
∴EG=FG=![]() AF,AF⊥DE,∠EGF=90°,
AF,AF⊥DE,∠EGF=90°,
∴此时,平行四边形EHFG是矩形;
故答案为:当平行四边形ABCD是矩形,平行四边形ABCD是矩形,并且AB=2AD.


科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图末-10,在平面直角坐标系中,直线y=x+1与y轴交于点A,与x轴交于点B,点C和点B关于y轴对称.
(1)求△ABC内切圆的半径;
(2)过O、A两点作⊙M,分别交直线AB、AC于点D、E,求证:AD+AE是定值,并求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
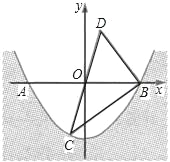
【题目】某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,点C关于原点O的对称点为点D,连接CD,BC,BD,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红爸爸上星期五买进某公司股票1000股,每股28元,下表为本周内每日该股票的涨跌情况。(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(1)通过上表你认为星期三收盘时,每股是多少?
(2)本周内每股最高是多少?最低是多少元?
(3)已知小红爸爸买进股票时付了![]() 的手续费,卖出时还需付成交额,
的手续费,卖出时还需付成交额,![]() 的手续费和
的手续费和![]() 的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>﹣3b;(3)7a﹣3b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
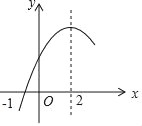
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,小王从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是小王从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
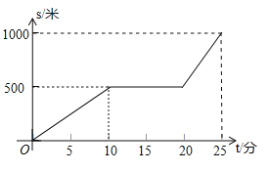
(1)小王从家到学校的路程共_________米,从家出发到学校,小王共用了________分钟;
(2)小王吃早餐用了____________分钟;
(3)小王吃早餐以前和吃完早餐后的平均速度分别是多少米/分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com