
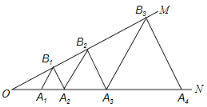
【题目】如图,已知:![]() ,点
,点![]() 、
、![]() 、
、![]() 在射线
在射线![]() 上,点
上,点![]() 、
、![]() 、
、![]() ...在射线
...在射线![]() 上,
上,![]() 、
、![]() 、
、![]() ...均为等边三角形,若
...均为等边三角形,若![]() ,则
,则![]() 的边长为__________.
的边长为__________.
【答案】![]()
【解析】
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4a,A4B4=8B1A2=8a,A5B5=16B1A2…进而得出答案
解:如图
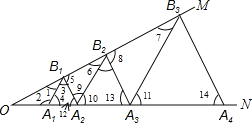
∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°-120°-30°=30°,
又∵∠3=60°,
∴∠5=180°-60°-30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=a,
∴A2B1=a,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4a,
A4B4=8B1A2=8a,
A5B5=16B1A2=16a,
以此类推:A6B6=32B1A2=32a.
故答案为:32a.


科目:初中数学 来源: 题型:
【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:

(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次排列的3个数:3,9,8,对任相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,![]() ,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,
,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,![]() ,
,![]() ,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,BF与CE相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)①若四边形EHFG是菱形,则平行四边形ABCD必须满足条件 ;
②若四边形EHFG是矩形,则平行四边形ABCD必须满足条件 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,□OABC的边OC在y轴的正半轴上,OC=3,A(2,1),反比例函数y=![]() (x>0)的图象经过点B.
(x>0)的图象经过点B.
(1)求点B的坐标和反比例函数的关系式;
(2)如图2,将线段OA延长交y=![]() (x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.
(x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边BC在x轴上,且∠ACB=90°.反比例函数y=![]() (x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
(x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
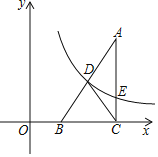
(1)求k的值;(2)若AE=BC,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,已知点A(0,2![]() ),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小:如改变,请说明理由;
(3)连接OQ,当OQ∥AB时,求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
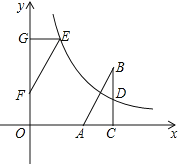
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com