
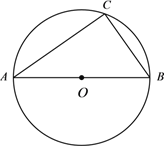
【题目】如图,已知在⊙O中,AB是⊙O的直径,AC=8,BC=6.
(1)求⊙O的面积;
(2)若D为⊙O上一点,且△ABD为等腰三角形,求CD的长.
【答案】(1)25π;(2)CD1=![]() ,CD2=7
,CD2=7![]()
【解析】分析:(1)利用圆周角定理的推论得到∠C是直角,利用勾股定理求出直径AB,再利用圆的面积公式即可得到答案;
(2)分点D在上半圆中点与点D在下半圆中点这两种情况进行计算即可.
详解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB是⊙O的直径,
∴AC=8,BC=6,
∴AB=10,
∴⊙O的面积=π×52=25π.
(2)有两种情况:
①如图所示,当点D位于上半圆中点D1时,可知△ABD1是等腰直角三角形,且OD1⊥AB,
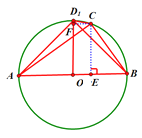
作CE⊥AB垂足为E,CF⊥OD1垂足为F,可得矩形CEOF,
∵CE=![]() ,
,
∴OF= CE=![]() ,
,
∴![]() ,
,
∵![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②如图所示,当点D位于下半圆中点D2时,
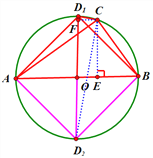
同理可求![]() .
.
∴CD1=![]() ,CD2=7
,CD2=7![]()


科目:初中数学 来源: 题型:
【题目】建设环境优美、文明和谐的新农村,某村村委会决定在村道两旁种植A,B两种树木,需要购买这两种树苗1000棵.A,B两种树苗的相关信息如下表:
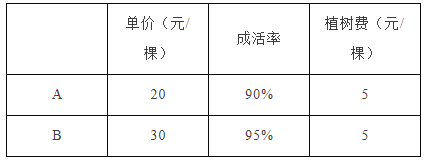
设购买A种树苗x棵,绿化村道的总费用为y元.解答下列问题:
(1)写出y(元)与x(棵)之间的函数关系式;
(2)若这批树苗种植后成活了925棵,则绿化村道的总费用需要多少元?
(3)若绿化村道的总费用不超过31000元,则最多可购买B种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
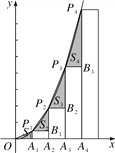
【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=![]() x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,则S3=________,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=________.
x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,则S3=________,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售![]() 、
、![]() 两种品牌的洗衣机,进价及售价如下表:
两种品牌的洗衣机,进价及售价如下表:
品牌 |
|
|
进价(元/台) | 1500 | 1800 |
售价(元/台) | 1800 | 2200 |
(1)该商场9月份用45000元购进![]() 、
、![]() 两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进
两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进![]() 、
、![]() 两种洗衣机的数量;
两种洗衣机的数量;
(2)该商场10月份又购进![]() 、
、![]() 两种品牌的洗衣机共用去36000元
两种品牌的洗衣机共用去36000元
①问该商场共有几种进货方案?请你把所有方案列出来;
②通过计算说明洗衣机全部销售完后哪种进货方案所获得的利润最大
查看答案和解析>>
科目:初中数学 来源: 题型:
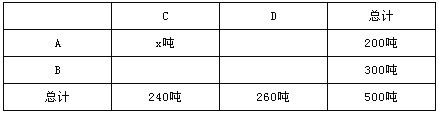
【题目】某乡A,B两村盛产香梨,A村有香梨200吨,B村有香梨300吨,现将这些香梨运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的香梨为x吨,A,B两村运香梨往两仓库的运输费用分别为yA元,yB元.
(1)请填写下表,并求出yA,yB与x之间的函数关系式;
(2)当x为何值时,A村的运费较少?
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A.B对应的数分别为﹣2和7,点M为数轴上一动点.
(1)请画出数轴,并在数轴上标出点A、点B;
(2)若点M到A的距离是点M到B的距离的两倍,我们就称点M是(A,B)的好点.
①若点M运动到原点O时,此时点M (A,B)的好点(填是或者不是)
②若点M以每秒1个单位的速度从原点O开始运动,当M是(B,A)的好点时,求点M的运动方向和运动时间
(3)试探究线段BM和AM的差即BM﹣AM的值是否一定发生变化?若变化,请说明理由:若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com