
【题目】如图在平面直角坐标系中,已知点A(0,2![]() ),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小:如改变,请说明理由;
(3)连接OQ,当OQ∥AB时,求P点的坐标.

【答案】(1)点B的坐标为B(3,![]() );(2)∠ABQ=90°,始终不变,理由见解析;(3)P的坐标为(﹣3,0).
);(2)∠ABQ=90°,始终不变,理由见解析;(3)P的坐标为(﹣3,0).
【解析】
(1)如图,作辅助线;证明∠BOC=30°,OB=2![]() ,借助直角三角形的边角关系即可解决问题;
,借助直角三角形的边角关系即可解决问题;
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题;
(3)根据点P在x的负半轴上,再根据全等三角形的性质即可得出结果
(1)如图1,过点B作BC⊥x轴于点C,
∵△AOB为等边三角形,且OA=2![]() ,
,
∴∠AOB=60°,OB=OA=2![]() ,
,
∴∠BOC=30°,而∠OCB=90°,
∴BC=![]() OB=
OB=![]() ,OC=
,OC=![]() =3,
=3,
∴点B的坐标为B(3,![]() );
);
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,
在△APO与△AQB中,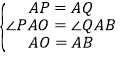 ,
,
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)如图2,∵点P在x轴负半轴上,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2![]() ,可求得BQ=3,
,可求得BQ=3,
由(2)可知,△APO≌△AQB,
∴OP=BQ=3,
∴此时P的坐标为(﹣3,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
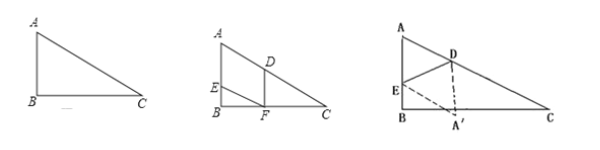
【题目】(本小题12分)如图1,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t的式子表示AE、AD的长;
(2)如图2,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)连接DE,当t为何值时,△DEF为直角三角形?
(4)如图3,连接DE,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形AEA′D为菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红爸爸上星期五买进某公司股票1000股,每股28元,下表为本周内每日该股票的涨跌情况。(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(1)通过上表你认为星期三收盘时,每股是多少?
(2)本周内每股最高是多少?最低是多少元?
(3)已知小红爸爸买进股票时付了![]() 的手续费,卖出时还需付成交额,
的手续费,卖出时还需付成交额,![]() 的手续费和
的手续费和![]() 的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲告诉张云:“距离地面越高,温度越低”,并给张云出示了下面的表格:
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 | -4 | -10 |
根据上表,父亲还给张云出了下面几个问题,请你和张云一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着![]() 的变化,
的变化,![]() 是怎么变化的?
是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,小王从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是小王从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
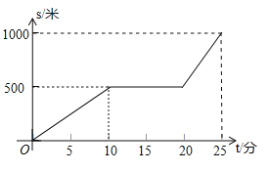
(1)小王从家到学校的路程共_________米,从家出发到学校,小王共用了________分钟;
(2)小王吃早餐用了____________分钟;
(3)小王吃早餐以前和吃完早餐后的平均速度分别是多少米/分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
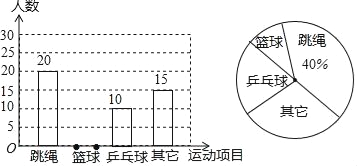
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设环境优美、文明和谐的新农村,某村村委会决定在村道两旁种植A,B两种树木,需要购买这两种树苗1000棵.A,B两种树苗的相关信息如下表:
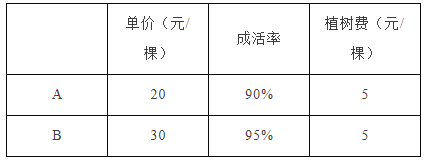
设购买A种树苗x棵,绿化村道的总费用为y元.解答下列问题:
(1)写出y(元)与x(棵)之间的函数关系式;
(2)若这批树苗种植后成活了925棵,则绿化村道的总费用需要多少元?
(3)若绿化村道的总费用不超过31000元,则最多可购买B种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡A,B两村盛产香梨,A村有香梨200吨,B村有香梨300吨,现将这些香梨运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的香梨为x吨,A,B两村运香梨往两仓库的运输费用分别为yA元,yB元.
(1)请填写下表,并求出yA,yB与x之间的函数关系式;
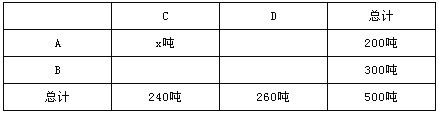
(2)当x为何值时,A村的运费较少?
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com